题目内容
如图，⊙O1与⊙O2交于点A，B，延长⊙O2的直径CA交⊙O1于点D，延长⊙O2的弦CB交⊙O1于点E．已知AC=6，AD：BC：BE=1：1：5，则DE的长是分析：连接公共弦AB，构成圆内接四边形ABED，根据圆内接四边形的性质，可证明△ABC∽△EDC，从而得出与AD、BC、BE有关的比例线段，根据AD：BC：BE=1：1：5，设线段长度，代入比例式可求CD、CE的长，在Rt△EDC中，用勾股定理求ED．
解答：
解：连接AB，在圆内接四边形ABED中，∠BAC=∠E，∠ABC=∠EDC，
因为AC为⊙O2直径，则∠ABC=90°，于是△ABC∽△EDC，
因为AD：BC：BE=1：1：5，
所以，设AD=x，BC=x，BE=5x；
于是：
=
，即6x2=36+6x，x2-x-6=0，
解得x=3，x=-2（负值设去），
在Rt△EDC中，ED=
=9
．
解：连接AB，在圆内接四边形ABED中，∠BAC=∠E，∠ABC=∠EDC，因为AC为⊙O2直径，则∠ABC=90°，于是△ABC∽△EDC，
因为AD：BC：BE=1：1：5，
所以，设AD=x，BC=x，BE=5x；
于是：
| 6 |
| 6x |
| x |
| 6+x |
解得x=3，x=-2（负值设去），
在Rt△EDC中，ED=
| 182-92 |
| 3 |
点评：本题考查的是对圆心角和圆周角的关系，以及圆的内接四边形的外角和相应的内对角关系的应用．解答此类题关键是通过角的关系，在解题中应用中间角来寻找等量关系．
练习册系列答案
相关题目
12、已知：如图，⊙O1与⊙O2外切于点P，直线AB过点P交⊙O1于A，交⊙O2于B，点C、D分别为⊙O1、⊙O2上的点，且∠ACP=65°，则∠BDP=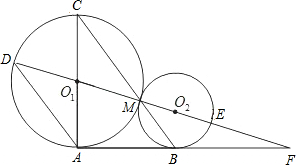
已知：如图，⊙O1与⊙O2外切于M点，AF是两圆的外公切线，A、B是切点，DF经过O1、O2，分别交⊙O1于D、⊙O2于E，AC是⊙O1的直径，BC经过M点，连接AD．
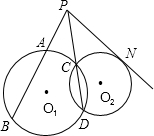如图，⊙O1与⊙O2相交于C、D两点，⊙O1的割线PAB与DC的延长线交于点P，PN与⊙O2相切于点N，若PB=10，AB=6，则PN=
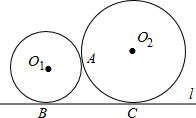已知：如图，⊙O1与⊙O2外切于A点，直线l与⊙O1、⊙O2分别切于B，C点，若⊙O1的半径r1=2cm，⊙O2的半径r2=3cm．求BC的长．
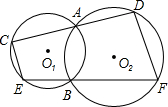已知如图：⊙O1与⊙O2相交于AB两点，过点A、B的直线分别与⊙O1交于C、E，与⊙O2交于D、F，连接CE、DF．