题目内容
如图,⊙O1、⊙O2外切于点P,它们的半径分别为4cm、1cm.直线l分别与⊙O1、⊙O2相切于A、B ,且与直线OlO2相交于T.求AB和BT的长.
,且与直线OlO2相交于T.求AB和BT的长.
分析:连接圆心和各个切点,得到一个直角梯形,再作梯形的另一高.得到直角三角形,根据锐角三角函数的知识和勾股定理进行求解.
解答: 解:连接O2B,O1A,作O2D⊥O1A.
解:连接O2B,O1A,作O2D⊥O1A.
∵直线l分别与⊙O1、⊙O2相切于A、B,
∴O1A⊥l,O2B⊥l,
又∵O2D⊥O1A,
∴四边形DABO2是矩形,
在直角三角形O2DO1中,O2O1=4+1=5,O1D=4-1=3,
根据勾股定理得O2D=4,
AB=O2D=4;
tan∠O1O2D=
,
即tan∠O1TA=
=
=
,则BT=
cm.
 解:连接O2B,O1A,作O2D⊥O1A.
解:连接O2B,O1A,作O2D⊥O1A.∵直线l分别与⊙O1、⊙O2相切于A、B,
∴O1A⊥l,O2B⊥l,
又∵O2D⊥O1A,
∴四边形DABO2是矩形,
在直角三角形O2DO1中,O2O1=4+1=5,O1D=4-1=3,
根据勾股定理得O2D=4,
AB=O2D=4;
tan∠O1O2D=
| 3 |
| 4 |
即tan∠O1TA=
| 3 |
| 4 |
| O1A |
| AT |
| O1A |
| AB+BT |
| 4 |
| 3 |
点评:此题综合运用了解直角三角形的知识和勾股定理.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
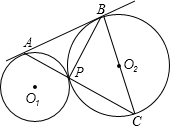 如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,
如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,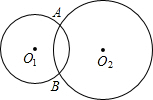 如图,⊙O1、⊙O2相交于点A、B,现给出4个命题:
如图,⊙O1、⊙O2相交于点A、B,现给出4个命题: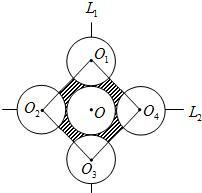 如图,⊙O1,⊙O2,⊙O3,⊙O4,⊙O的半径均为2cm,⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,并且圆心分别位于两条互相垂直的直线L1,L2上,连接O1,O2,O3,O4得四边形O1O2O3O4,则图中阴影部分的面积为
如图,⊙O1,⊙O2,⊙O3,⊙O4,⊙O的半径均为2cm,⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,并且圆心分别位于两条互相垂直的直线L1,L2上,连接O1,O2,O3,O4得四边形O1O2O3O4,则图中阴影部分的面积为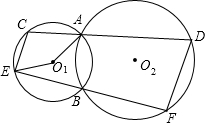 已知:如图,⊙O1和⊙O2相交于A、B两点,经过A的直线CD与⊙O1交于点C、与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F,连接CE、DF.若∠AO1E=100°,则∠D的度数为
已知:如图,⊙O1和⊙O2相交于A、B两点,经过A的直线CD与⊙O1交于点C、与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F,连接CE、DF.若∠AO1E=100°,则∠D的度数为 (1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )
(1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )