题目内容
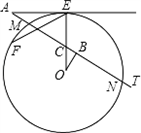
如图，AT切⊙O于T，直线AO交⊙O于B、C且∠TAB=40°，则∠C的度数为
- A.25°
- B.30°
- C.40°
- D.50°
A
分析：连接OT，则OT⊥AT，由∠TAB=40°，得∠AOT=50°，再根据OC=OT得出∠C=∠OTC，从而得出答案．
解答：
解：连接OT，
∵AT切⊙O于T，
∴OT⊥AT，
∴∠ATO=90°，
∵∠TAB=40°，∴∠AOT=50°，
∵OC=OT，∴∠C=∠OTC，
∵∠AOT=∠C+∠OTC，
∴∠C=25°．
故选A．
点评：本题考查了切线的性质、圆周角定理，是基础知识要熟练掌握．
分析：连接OT，则OT⊥AT，由∠TAB=40°，得∠AOT=50°，再根据OC=OT得出∠C=∠OTC，从而得出答案．
解答：
解：连接OT，∵AT切⊙O于T，
∴OT⊥AT，
∴∠ATO=90°，
∵∠TAB=40°，∴∠AOT=50°，
∵OC=OT，∴∠C=∠OTC，
∵∠AOT=∠C+∠OTC，
∴∠C=25°．
故选A．
点评：本题考查了切线的性质、圆周角定理，是基础知识要熟练掌握．
练习册系列答案
名校课堂系列答案
相关题目
，MN=2
如图，AT切⊙O于T，直线AO交⊙O于B、C且∠TAB=40°，则∠C的度数为（ ）
，MN=2
．
是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比．