��Ŀ����
��ͼ��AE�С�O�ڵ�E��AT����O�ڵ�M��N���߶�OE��AT�ڵ�C��OB��AT�ڵ�B����֪
��EAT=30�㣬AE=3 ��MN=2
��MN=2 ��
��
��1�����COB�Ķ�����
��2�����O�İ뾶R��
��3����F�ڡ�O�ϣ� ���ӻ�������EF=5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�
���ӻ�������EF=5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�
��EAT=30�㣬AE=3
 ��MN=2
��MN=2 ��
����1�����COB�Ķ�����
��2�����O�İ뾶R��
��3����F�ڡ�O�ϣ�
 ���ӻ�������EF=5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�
���ӻ�������EF=5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�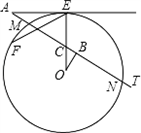
| �⣺��1����AE�С�O�ڵ�E�� ��AE��CE����OB��AT�� ���AEC=��CBO=90�㣬 �֡�BCO=��ACE�� ���AEC�ס�OBC���֡�A=30�㣬 ���COB=��A=30�㣻 ��2����AE=3  ����A=30�㣬 ����A=30�㣬����Rt��AEC�У�tanA=tan30��=  ����EC=AEtan30��=3�� ����EC=AEtan30��=3����OB��MN�� ��BΪMN���е㣬��MN=2  �� ����MB=  MN= MN=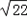 �� ������OM���ڡ�MOB�У�OM=R��MB=  �� ����OB=  = = �� ���ڡ�COB�У���BOC=30�㣬 ��cos��BOC=cos30��=  = = �� ����BO=  OC�� OC����OC=  OB= OB=  �� ����OC+EC=OM=R�� ��R=   +3�� +3�������ã�R2+18R��115=0�� ����R+23����R��5��=0�� ��ã�R=��23����ȥ����R=5�� ��R=5�� ��3����EFͬһ�࣬��COB����ƽ�ơ���ת�����Ʊ任�� ��������������6���� ��ͼ��ÿСͼ2����������Բ�ϵ������Σ�����ͼ��ʾ�� �ӳ�EO��ԲO�ڵ�D������DF�� ��ͼ��ʾ�� ��EF=5��ֱ��ED=10���ɵó���FDE=30�㣬 ��FD=5  �� ����C��EFD=5+10+5  =15+5 =15+5 �� ���ɣ�2���ɵ�C��COB=3+  �� ����C��EFD��C��COB=��15+5  ������3+ ������3+ ��=5��1�� ��=5��1�� |
|

��ϰ��ϵ�д�
�����Ŀ


 ��MN=2
��MN=2


 ��MN=2
��MN=2 ��
�� ���ӻ�������EF=5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�
���ӻ�������EF=5���ѡ�OBC����ƽ�ơ���ת�����Ʊ任��ʹ������������ֱ����E��F�غϣ���EF��ͬһ�࣬�����������ι��ж��ٸ��������������ҳ���һ�������ڡ�O�ϵ�������������ͼ�л�����������Σ������������������OBC���ܳ�֮�ȣ�