题目内容
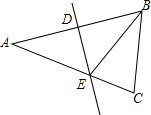 如图,AB=AC,AB的垂直平分线交AB于D,交AC于E,BE恰好平分∠ABC,有以下结论:
如图,AB=AC,AB的垂直平分线交AB于D,交AC于E,BE恰好平分∠ABC,有以下结论:(1)ED=EC;(2)△ABC的周长等于2AE+EC;(3)图中共有3个等腰三角形;(4)∠A=36°,
其中正确的共有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
考点:线段垂直平分线的性质,等腰三角形的判定与性质
专题:
分析:(1)由角平分线的性质可判定ED≠EC;(2)由垂直平分线的性质可知AE=EB,则有AE+EB+AB=AE+AE+AE+EC=3AE+EC,可判断出(2);(3)可判定△ABE、△ABC、△BEC为等腰三角形;(4)由(3)可求得∠A;可得出答案.
解答:解:(1)由题意可知DE⊥AB,BE平分∠ABC,
∴当EC⊥BC时,有ED=EC,
∵AB=AC,
∴∠ACB不可能等于90°,
∴ED=EC不正确;
(2)∵E在线段AB的垂直平分线上,
∴EA=EB,
∴EA+EB+AB=EA+EA+AB=2EA+AB,
∵AB=AC,且AC=AE+EC,
∴EA+EB+AB=3AE+EC,
∴(2)不正确;
(3)∵AB=AC,
∴△ABC为等腰三角形,∠C=∠ABC,
∵EA=EB,
∴△EAB为等腰三角形,∠A=∠ABE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠C=2∠CBE,
又∠BEC=∠A+∠ABE=2∠CBE,
∴∠BEC=∠C,
∴BE=BC,
∴△BEC为等腰三角形,
∴图中共有3个等腰三角形,
∴(3)正确;
(4)由(3)可得∠BEC=∠C=2∠EBC,
∴2∠EBC+2∠EBC+∠EBC=180°,
∴∠EBC=36°,
∴∠A=∠ABE=∠EBC=36°,
∴(4)正确;
∴正确的有(3)(4)共两个,
故选C.
∴当EC⊥BC时,有ED=EC,
∵AB=AC,
∴∠ACB不可能等于90°,
∴ED=EC不正确;
(2)∵E在线段AB的垂直平分线上,
∴EA=EB,
∴EA+EB+AB=EA+EA+AB=2EA+AB,
∵AB=AC,且AC=AE+EC,
∴EA+EB+AB=3AE+EC,
∴(2)不正确;
(3)∵AB=AC,
∴△ABC为等腰三角形,∠C=∠ABC,
∵EA=EB,
∴△EAB为等腰三角形,∠A=∠ABE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠C=2∠CBE,
又∠BEC=∠A+∠ABE=2∠CBE,
∴∠BEC=∠C,
∴BE=BC,
∴△BEC为等腰三角形,
∴图中共有3个等腰三角形,
∴(3)正确;
(4)由(3)可得∠BEC=∠C=2∠EBC,
∴2∠EBC+2∠EBC+∠EBC=180°,
∴∠EBC=36°,
∴∠A=∠ABE=∠EBC=36°,
∴(4)正确;
∴正确的有(3)(4)共两个,
故选C.
点评:本题主要考查线段垂直平分线的性质和等腰三角形的判定和性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键,注意三角形内角和定理的应用.

练习册系列答案
相关题目
cos60°=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列条件中,不能判断△ABC为直角三角形的是( )
| A、∠B=∠C-∠A | ||
| B、a2=(b+c)(b-c) | ||
| C、∠A:∠B:∠C=3:4:5 | ||
D、a=1,b=2,c=
|