题目内容
【题目】在
中 ，
平分
交
于
，
的两边分别与
, 
相交于
，
两点，且
.
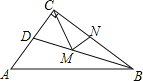
（1）如图，若
， 
，
，
，
.
①写出
°，的长是 .
②求四边形
的周长.
（2）如图，过作
于
，作
于
，先补全图乙再证明
.
【答案】（1）①90°，18，②30；（2）作图见解析，证明见解析
【解析】
（1）①由直角三角形两锐角互余可得
，结合直角三角形30度角的性质可得AB长，由平行的性质及角平分线的性质可得
，易得
的度数；②在①的基础上，结合等角对等边的性质可得
，
设
，根据直角三角形30度角的性质可得
，则
，
可得AM、MD、DN、AN的长，易得四边形
的周长；
（3）利用HL定理可证
≌
，
，结合全等三角形对应边相等的性质易证
.
解：①解：∵
, 
∴
∵
∴
，
又
∴
∴
又∵
平分
∴
∴
,
所以
90°，
的长是18.
②解：∵,
∴
∵
∴，
又
∴
∴
又∵平分
∴
∴
∴
在
中，设，则
∴
中, 
∴
∴
∴
∴
，
所以四边形的周长=
（2）补全图如图所示
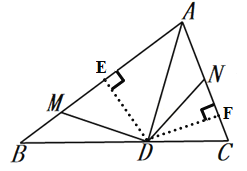
证明：由作图知，
，
由已知，平分，
∴ ≌
又
.
练习册系列答案
相关题目
