题目内容
如图，Rt△ABC的两直角边AC=8cm，BC=6cm，D为AC上一点，将△ABC折叠，使点A与点B重合，折痕为DE，则CD的长为________cm．
分析：设CD=x，先根据翻折变换的性质可得到AD=BD，则BD=8-x，再根据勾股定理即可求解．
解答：设CD=x，则BD=8-x，
∵△BDE是△ADE沿直线DE翻折而成，
∴AD=BD=8-x，
∵△BCD是直角三角形，
∴BC2=BD2-CD2，即62=（8-x）2-x2，
解得x=
．故答案为：
．点评：本题主要考查了折叠问题和勾股定理的综合运用．解题过程中应注意折叠是一种对称变换，它属于轴对称，对应边和对应角分别相等．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
如图，Rt△ABC的直角边BC在x轴正半轴上，斜边AC边上的中线BD反向延长线交y轴负半轴于E，双曲线
如图，Rt△ABC的两直角边分别为1，2，以Rt△ABC的斜边AC为一直角边，另一直角边为1画第二个△ACD；在以△ACD的斜边AD为一直角边，另一直角边长为1画第三个△ADE；…，依此类推，第n个直角三角形的斜边长是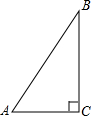
如图，Rt△ABC的斜边AB=10cm，
如图，Rt△ABC的一条直角边AB是⊙O的直径，AB=8，斜边交⊙O于D，∠A=30°，求阴影部分的面积．