题目内容
在正方形ABCD中有一点E，△EAB是等边三角形，∠CED为（ ）A．60°
B．75°
C．120°
D．150°
【答案】分析：根据正方形的性质和△EAB为等腰三角形，可推出∠EAB=∠EBA=∠AEB=60°，AE=AC=BE=BD，从而得出：∠AEC=∠DEB=75°，∠CED=150°．
解答：
解：如图，连接CE，DE
∵△EAB是等边三角形，正方形ABCD，
∴∠EAB=∠EBA=∠AEB=60°，AE=AD=BE=BD
∴∠EAC=∠DBE=30°，∠AEC=∠DEB=75°
∴∠CED=360°-75°-75°-60°=150°
故选D．
点评：本题考查等边三角形的性质，其三边相等，三个内角相等，均为60°．
解答：
解：如图，连接CE，DE∵△EAB是等边三角形，正方形ABCD，
∴∠EAB=∠EBA=∠AEB=60°，AE=AD=BE=BD
∴∠EAC=∠DBE=30°，∠AEC=∠DEB=75°
∴∠CED=360°-75°-75°-60°=150°
故选D．
点评：本题考查等边三角形的性质，其三边相等，三个内角相等，均为60°．
练习册系列答案
相关题目
如图，在正方形ABCD中有一点E，把△ABE绕点B旋转到△CBF，连接EF，则△EBF的形状是（ ）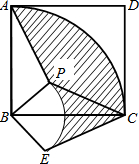
如图，在正方形ABCD中有一点P，连接AP、BP，旋转△APB到△CEB的位置．
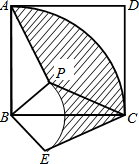如图，在正方形ABCD中有一点P，连接AP、BP，旋转△APB到△CEB的位置．