题目内容
已知三角形ABC中,AB=AC,点A,B,C在以O为圆心的同一个圆上,圆心O到BC的距离为3cm,圆的半径为7cm,求腰长AB.
分析:可根据勾股定理先求得BD的值,再根据勾股定理可求得AB的值.注意:圆心在内接三角形内时,AD=10cm;圆心在内接三角形外时,AD=4cm.
解答:解:分圆心在内接三角形内和在内接三角形外两种情况讨论,
如图一,假若∠A是锐角,△ABC是锐角三角形,

连接OA,OB,
∵OD=3cm,OB=7cm,
∴AD=10cm,
∴BD=
=2
cm,
∵OD⊥BC,根据垂径定理和等腰三角形的性质可得,AD⊥BC,
∴AD=
=2
cm;
如图二,若∠A是钝角,则△ABC是钝角三角形,
和图一解法一样,只是AD=7-3=4cm,
∴AB=
=2
cm,
综上可得腰长AB=2
cm或2
cm.
如图一,假若∠A是锐角,△ABC是锐角三角形,

连接OA,OB,
∵OD=3cm,OB=7cm,
∴AD=10cm,
∴BD=
| OB2-OD2 |
| 10 |
∵OD⊥BC,根据垂径定理和等腰三角形的性质可得,AD⊥BC,
∴AD=
| AD2+BD2 |
| 35 |
如图二,若∠A是钝角,则△ABC是钝角三角形,
和图一解法一样,只是AD=7-3=4cm,
∴AB=
| AD2+BD2 |
| 14 |
综上可得腰长AB=2
| 35 |
| 14 |
点评:此题主要考查了垂径定理和勾股定理,注意分圆心在内接三角形内和在内接三角形外两种情况讨论,有一定难度.

练习册系列答案
相关题目
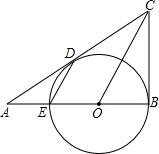 点E,与AC切于点D.
点E,与AC切于点D. 6、如图,已知三角形ABC中,AB=AC,∠C=30°,AD⊥AB,且AD=4.8cm,则CD=
6、如图,已知三角形ABC中,AB=AC,∠C=30°,AD⊥AB,且AD=4.8cm,则CD= 如图,已知三角形△ABC中,∠A=90°,AB=3,BC=6.
如图,已知三角形△ABC中,∠A=90°,AB=3,BC=6.