题目内容
 如图,OC是∠AOB的平分线,OD是∠COB的平分线,∠AOD=60°,则∠AOB=
如图,OC是∠AOB的平分线,OD是∠COB的平分线,∠AOD=60°,则∠AOB=分析:根据OC是∠AOB的平分线,OD是∠COB的平分线,得∠AOC=
∠AOB,∠COD=
∠AOB,又有∠AOD=∠AOC+∠COD,即可得出∠AOB的度数.
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:∵OC是∠AOB的平分线
∴∠AOC=∠BOC=
∠AOB
∵OD是∠COB的平分线
∴∠COD=
∠BOC=
∠AOB
∴∠AOD=∠AOC+∠COD=
∠AOB+
∠AOB=60°
∴∠AOB=80°.
故答案为80°.
∴∠AOC=∠BOC=
| 1 |
| 2 |
∵OD是∠COB的平分线
∴∠COD=
| 1 |
| 2 |
| 1 |
| 4 |
∴∠AOD=∠AOC+∠COD=
| 1 |
| 2 |
| 1 |
| 4 |
∴∠AOB=80°.
故答案为80°.
点评:本题主要考查角的比较与运算和角平分线的定义,比较简单.

练习册系列答案
相关题目
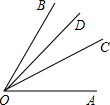 如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )
如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )A、∠COD=
| ||
B、∠AOD=
| ||
C、∠BOD=
| ||
D、∠BOC=
|

 13、如图,OC是∠AOB的平分线,点D是OC上的一点,DE⊥OA于点E,DF⊥OB于点F,连接EF,交OC于点P,把这个图形沿OC对折后观察,除∠AOC=∠BOC外,你还可以发现的结论是
13、如图,OC是∠AOB的平分线,点D是OC上的一点,DE⊥OA于点E,DF⊥OB于点F,连接EF,交OC于点P,把这个图形沿OC对折后观察,除∠AOC=∠BOC外,你还可以发现的结论是 22、(1)画出下图的三视图.
22、(1)画出下图的三视图. 25、如图,OC是∠AOB的平分线,且∠AOD=90°.
25、如图,OC是∠AOB的平分线,且∠AOD=90°.