题目内容
17.关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根都在-1和0之间(不包括-1和0),则a的取值范围是$-\frac{9}{4}$<a<-2.分析 首先根据根的情况利用根的判别式解得a的取值范围,然后根据根两个不相等的实数根都在-1和0之间(不包括-1和0),结合函数图象确定其函数值的取值范围得a,易得a的取值范围.
解答 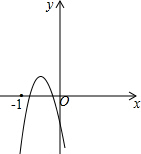 解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根
解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根
∴△=(-3)2-4×a×(-1)>0,
解得:a>$-\frac{9}{4}$
设f(x)=ax2-3x-1,如图,
∵实数根都在-1和0之间,
∴-1$<-\frac{-3}{2a}<0$,
∴a$<-\frac{3}{2}$,
且有f(-1)<0,f(0)<0,
即f(-1)=a×(-1)2-3×(-1)-1<0,f(0)=-1<0,
解得:a<-2,
∴$-\frac{9}{4}$<a<-2,
故答案为:$-\frac{9}{4}$<a<-2.
点评 本题主要考查了一元二次方程根的情况的判别及抛物线与x轴的交点,数形结合确定当x=0和当x=-1时函数值的取值范围是解答此题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
8.某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:如果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,根据四人各自的平均成绩,公司将录取乙.
| 候选人 | 甲 | 乙 | 丙 | 丁 | |
| 测试成绩(百分制) | 面试 | 86 | 92 | 90 | 83 |
| 笔试 | 90 | 83 | 83 | 92 | |
5.甲型流感病毒的直径大约为0.0000000081米,用科学记数法表示为( )
| A. | 0.81×10-9米 | B. | 0.81×10-8米 | C. | 8.1×10-7米 | D. | 8.1×10-9米 |
12.在一个不透明的盒子中装有a个除颜色外完全相同的球,这a个球中只有3个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值约为( )
| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
2. 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简|a-b|+|a+b|的结果为( )
实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简|a-b|+|a+b|的结果为( )
 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简|a-b|+|a+b|的结果为( )
实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简|a-b|+|a+b|的结果为( )| A. | 2a | B. | 2b | C. | -2a | D. | -2b |
6.某种超级计算机完成一次基本运算的时间约为0.00000000000011秒,用科学记数法表示这个数为( )
| A. | 1.1×10-12 | B. | 1.1×10-13 | C. | 11×10-12 | D. | 11×10-13 |