题目内容
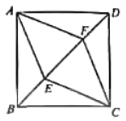
【题目】如图，在正方形ABCD中，点E，F在对角线BD上，
，迎接AF，CE.
（1）求证：
；
（2）试判断四边形AECF的形状，并说明理由.
【答案】（1）证明见解析；（2）菱形，理由见解析.
【解析】
（1）根据正方形的性质可得：
，
，然后根据平行线的性质可得：
和
，从而证出
，最后利用AAS即可证出
；
（2）根据全等三角形的性质可得: 
,再根据平行四边形的判定可得：四边形AECF是平行四边形，然后利用SAS即可证出
，从而得出
，最后根据菱形的判定即可证出四边形AECF是菱形.
解：（1）∵四边形ABCD是正方形
∴，
∴
∵
∴
∵
，
∴
∴在
与
中
∴
（2）四边形AECF是菱形，理由如下，
∵
∴，
∵
∴四边形AECF是平行四边形
在
与
中
∴
∴
∴四边形AECF是菱形
练习册系列答案
相关题目
