题目内容
1.解不等式组$\left\{\begin{array}{l}2x+4≤5(x+2)\\ x-1<\frac{2}{3}x.\end{array}\right.$把它的解集在数轴上表示出来,并求它的整数解.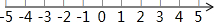
分析 分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:$\left\{\begin{array}{l}{2x+4≤5(x+2)①}\\{x-1<\frac{2}{3}x②}\end{array}\right.$,
由①得x≥-2,
由②得x<3.
不等式组的解集在数轴上表示如下:
故原不等式组的解集为-2≤x<3.
故原不等式组的整数解为-2,-1,0,1,2.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
12.下列命题:
①两点确定一条直线;②两点之间,线段最短;③对顶角相等;④内错角相等;
其中真命题的个数是( )
①两点确定一条直线;②两点之间,线段最短;③对顶角相等;④内错角相等;
其中真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.抛物线y=-(x+2)2-3向右平移了3个单位,那么平移后抛物线的顶点坐标是( )
| A. | (-5,-3) | B. | (-2,0) | C. | (-1,-3) | D. | (1,-3) |
13.分式$\frac{1}{3{a}^{2}b}$与$\frac{1}{8a{b}^{2}}$的最简公分母是( )
| A. | 24a2b2 | B. | 24a3b3 | C. | 24a3b2 | D. | 24a2b3 |