题目内容
8.若A(-1,m)与B(2,m-3)是反比例函数y=$\frac{k}{x}$图象上的两个点,则m=2.分析 根据反比例函数图象上点的坐标特征得-m=k,2(m-3)=k,消掉k得到-m=2(m-3),然后解关于m的一元一次方程即可.
解答 解:把A(-1,m)与B(2,m-3)分别代入反比例函数y=$\frac{k}{x}$得:-m=k,2(m-3)=k,
∴-m=2(m-3),
解得m=2.
故答案为2.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
18.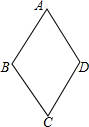 如图,四边形ABCD的四边相等,且面积为120cm2,对角线AC=24cm,则四边形ABCD的周长为( )
如图,四边形ABCD的四边相等,且面积为120cm2,对角线AC=24cm,则四边形ABCD的周长为( )
 如图,四边形ABCD的四边相等,且面积为120cm2,对角线AC=24cm,则四边形ABCD的周长为( )
如图,四边形ABCD的四边相等,且面积为120cm2,对角线AC=24cm,则四边形ABCD的周长为( )| A. | 52cm | B. | 40cm | C. | 39cm | D. | 26cm |
3.已知弹簧在一定限度内,它的长度y(厘米)与所挂重物质量x(千克)是一次函数关系.表中记录的是两次挂不同重量重物的质量(在弹性限度内)与相对应的弹簧长度.
求不挂重物时弹簧的长度.
| 所挂重物质量x(千克) | 2.5 | 5 |
| 弹簧长度y(厘米) | 7.5 | 9 |
18.同时抛掷三枚质地均匀的硬币,至少有两枚硬币正面向上的概率是( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
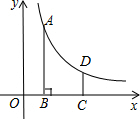 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD=$\frac{4}{3}$
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD=$\frac{4}{3}$