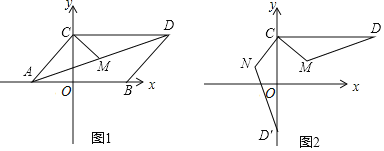Question

【题目】我们约定：对角线互相垂直的凸四边形叫做“正垂形”．

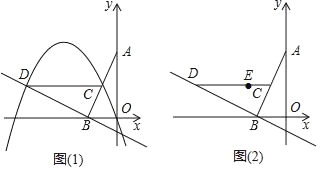
（1）①在“平行四边形，矩形，菱形，正方形”中，一定是“正垂形”的有　 　；

②在凸四边形ABCD中，AB=AD且CB≠CD，则该四边形　 　“正垂形”．（填“是”或“不是”）

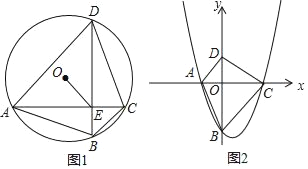
（2）如图1，A，B，C，D是半径为1的⊙O上按逆时针方向排列的四个动点，AC与BD交于点E，∠ACB﹣∠CDB=∠ACD﹣∠CBD，当≤OE≤时，求AC2+BD2的取值范围；

（3）如图2，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a，b，c为常数，a＞0，c＜0）与x轴交于A，C两点（点A在点C的左侧），B是抛物线与y轴的交点，点D的坐标为（0，﹣ac），记“正垂形”ABCD的面积为S，记△AOB，△COD，△AOD，△BOC的面积分别为S1，S2，S3，S4．试直接写出满足下列三个条件的抛物线的解析式；

①； ②； ③“正垂形”ABCD的周长为12．

Answer 1

【答案】（1）①菱形、正方形；②不是；（2）6≤AC2+BD2≤7；（3）y=x2﹣9．

【解析】

（1）①∵菱形、正方形的对角线相互垂直，∴菱形、正方形为“正垂形”，故：答案是：菱形、正方形；

②如图，当BC=CD时，AB=AD，AC=AC，∴△ABC≌△ADC，可知，四边形ABCD不是“正垂形；

（2）由∠ACB-∠CDB=∠ACD-∠CBD，可知AC⊥BD；OE2=OM2+ON2=（AC）2+（BD）2=（AC2+BD2），即可求解；

（3）设：△=b2-4ac，则：A（，0）、B（0，c）、C（，0）、D（0，-ac），由=+；=+，求a=1；由=+求得b=0；则四边形ABCD为菱形，即：4AD=12，即可求解．

解：（1）①∵菱形、正方形的对角线相互垂直，∴菱形、正方形为“正垂形”，

∵平行四边形、矩形对角线不垂直，∴它们不是“正垂形”，

故：答案是：菱形、正方形；

②如图，当BC=CD时，AB=AD，AC=AC，∴△ABC≌△ADC，

∴∠BAC=∠DAC，∵AB=AD，∴AC⊥BD，

∴当CB≠CD时，四边形ABCD不是“正垂形”，

故：答案为：不是；

（2）∵∠ACB﹣∠CDB=∠ACD﹣∠CBD，而∠ACB=∠ABD，∠ACD=∠ABD，

即：∠ABD+∠BDC=∠DBC+∠ADB，而：∠ABD+∠BDC=∠DBC+∠ADB=180°，

∴∠ACB+∠DBC=∠BDC+∠ACD=90°，∴AC⊥BD；

如下图：过点O分别作AC、BD的垂线，垂足为M、N，连接OA、OD，

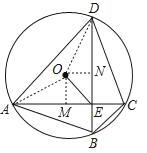
OE2=OM2+ON2=（AC）2+（BD）2=（AC2+BD2），

把≤OE≤，代入上式得：

6≤AC2+BD2≤7；

（3）设：△=b2﹣4ac，则：A（，0）、B（0，c）、C（，0）、D（0，﹣ac），

OA=，OB=﹣c，OC=，OD=﹣ac，BD=﹣ac﹣c，

S=ACBD=﹣（ac+c），S1=OAOB=﹣，S2=OCOD=﹣，

S3=OAOD=﹣，S4=OBOC=﹣，

=+，=+， 即：+=+；

∴，即a=1，

则：S=﹣c，s1=﹣，S4=，

∵=+，∴S=S1+S2+2，

∴﹣c=﹣+2，解得：b=0，

∴A（﹣，0）B（0，c）C（，0）D（0，﹣c），

∴四边形ABCD为菱形，即：4AD=12，

∵AD2=c2﹣c，解得：c=﹣9或10（舍去），

即：y=x2﹣9．