Question

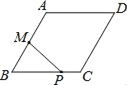
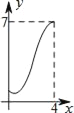
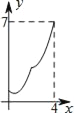
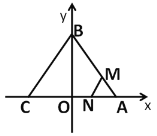
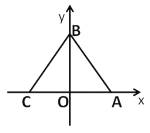
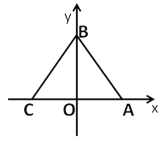
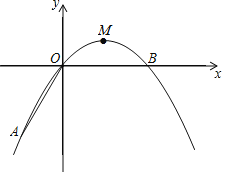
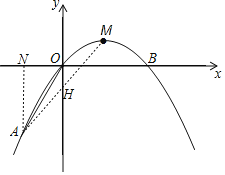
【题目】如图，已知在平面直角坐标系xOy中，顶点为M的抛物线C1：y＝ax2+bx（a＜0）经过点A和x轴上的点B，AO＝OB＝2，∠AOB＝120°．

（1）求该抛物线的表达式；

（2）连结AM，求S△AOM；

（3）设点F是x轴上一点，如果△MBF与△AOM相似，求所有符合条件的点F的坐标．

Answer 1

【答案】（1）y＝﹣x2+；（2）S△AOM＝；（3）点F的坐标为：（4，0）或（，0）．

【解析】

（1）过点A作AN⊥x轴于点N，则∠AON＝60°，ON＝OA＝1，AN＝，故点A（﹣1，﹣），利用待定系数法即可求解；

（2）连接AM交y轴于点H，求出直线AM的表达式，得到OH的长，然后根据S△AOM＝OH·（xM﹣xA）进行计算；

（3）分两种情况：①当∠BMF＝150°时，可得三角形不存在，此情况舍去；②当∠MBF＝150°时，再分△OAM∽△BMF和△OAM∽△BFM，分别利用相似三角形的性质列出比例式求出BF即可．

解：（1）过点A作AN⊥x轴于点N，

∵∠AOB＝120°，

∴∠AON＝60°，

∴ON＝OA＝1，AN＝，

故点A（﹣1，﹣），

将点A、B的坐标代入抛物线表达式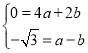得：，解得：，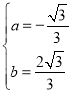

故抛物线的表达式为：y＝﹣x2+；

（2）连接AM交y轴于点H，

∵y＝﹣x2+，

∴M（1，），

设直线AM的表达式为：y＝kx＋b（k≠0），

将点A、M的坐标代入一次函数的表达式得：，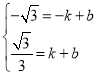

解得：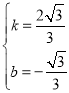

∴直线AM的表达式为：y＝x﹣，

∴OH＝，

∴S△AOM＝OH·（xM﹣xA）＝××2＝；

（3）∵A（﹣1，﹣），B（2，0），M（1，），

∴，，，

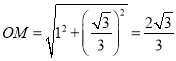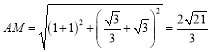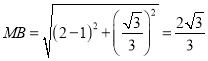∴∠MOB＝∠MBO＝30°，

∴∠AOM＝150°，

①当∠BMF＝150°时，∠BFM＝0°，三角形不存在，故此情况舍去；

②当∠MBF＝150°，且△OAM∽△BMF时，

则，即，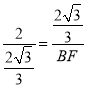

解得：BF＝；

当∠MBF＝150°，且△OAM∽△BFM时，

同理可得：BF＝2，

故点F的坐标为：（，0）或（4，0）；