Question

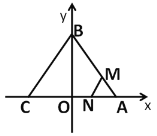
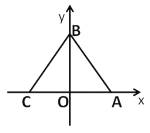
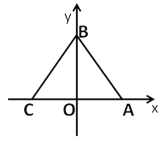
【题目】如图，已知△ABC的顶点坐标分别为A(3，0)，B(0，4)，C(-3，0)，动点M，N同时从A点出发，N沿A→C，M沿折线A→B→C，均以每秒1个单位长度的速度移动，当一个动点到达终点C时，另一个动点也随之停止移动，移动时间记为t秒．连接MN．

（1）移动过程中，将△ABC沿直线MN折叠，若点A恰好落在BC边上的点D处，求此时t的值．

（2）当点M，N移动时，记△ABC在直线MN右侧部分的面积为S，求S关于时间t的函数关系式．

Answer 1

【答案】（1）；（2）

【解析】

（1）证得四边形是菱形，根据相似三角形的性质得到，即可解决问题；
（2）分两种情形当0＜t≤5时，△ABC在直线MN右侧部分是△AMN；②当5＜t≤6时，△ABC在直线MN右侧部分是四边形ABNM；分别求解即可．

（1）由折叠可知，，

∴，

∴四边形是菱形，

∴，

∴，

∴，

∵，，，

∴，，，

∴，

∴，

解得：；

（2）作于点，

①当时，

∵，

，

∴，

∴，即，

∴，

∴；

②当时，

∵，

，

∴，

∴，即，

∴，

∵，

∴

，

，

∴

．