题目内容
3. 如图,在Rt△ABC中,∠ABC=90°,∠B=60°,BC=2,△A′B′C是由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A,B′,A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ABC=90°,∠B=60°,BC=2,△A′B′C是由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A,B′,A′在同一条直线上,则AA′的长为( )| A. | 6 | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 3 |
分析 根据题意先求出∠BAC=30°,再根据含30度的直角三角形三边的关系得到AB=2BC=4,再根据旋转的性质得A′B′=AB=4,B′C=BC=2,A′C=AC,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,得出△CAA′为等腰三角形,从而得出∠CAA′=∠A′=30°,再利用三角形外角性质计算出∠B′CA=30°,可得B′A=B′C=2,然后根据AA′=AB′+A′B′进行计算即可得出答案.
解答 解:∵∠ACB=90°,∠B=60°,
∴∠BAC=30°,
∵BC=2
∴AB=4,
∵△ABC绕点C顺时针旋转得到△A′B′C′,
∴A′B′=AB=4,B′C=BC=2,A′C=AC,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,
∴△CAA′为等腰三角形,
∴∠CAA′=∠A′=30°,
∵A、B′、A′在同一条直线上,
∴∠A′B′C=∠B′AC+∠B′CA,
∴∠B′CA=60°-30°=30°,
∴B′A=B′C=2,
∴AA′=AB′+A′B′=4+2=6.
故选A.
点评 本题考查了旋转的性质:掌握对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等是本题的关键.也同时考查了含30度的直角三角形三边的关系.

练习册系列答案
相关题目
13.小成本喜剧片《人在囧途之泰囧》上映不到一个月,票房已经突破13亿,仅次于好莱坞大片《阿凡达》在中国创造的14亿票房成绩,成为华语片票房之王.用科学记数法表示13亿为( )
| A. | 0.13×1010元 | B. | 1.3×109元 | C. | 1.3×1010元 | D. | 13×109元 |
11.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为80分、85分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
| A. | 255分 | B. | 84.5分 | C. | 85.5分 | D. | 86.5分 |
18.在下面四个几何体中,俯视图是三角形的是( )
| A. |  | B. | 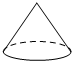 | C. | 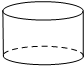 | D. | 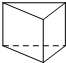 |
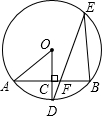 如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上. 如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE.求证:∠A=∠D.
如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE.求证:∠A=∠D.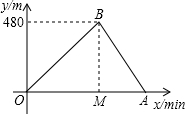 小志和小明选择一个土坡进行跑步训练,他们按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚,两人上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍,设两人出发xmin后距出发点的距离为ym,图中折线表示小志在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
小志和小明选择一个土坡进行跑步训练,他们按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚,两人上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍,设两人出发xmin后距出发点的距离为ym,图中折线表示小志在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).