题目内容
19.先化简,再求值:($\frac{{x}^{2}-3x+6}{x+2}$-1)÷$\frac{{x}^{2}-4}{{x}^{2}+4x+4}$,其中x=2+$\sqrt{5}$.分析 首先通分计算小括号里的算式,然后把除法转化成乘法进行约分计算,最后再把x=2+$\sqrt{5}$代入计算即可.
解答 解:($\frac{{x}^{2}-3x+6}{x+2}$-1)÷$\frac{{x}^{2}-4}{{x}^{2}+4x+4}$
=($\frac{{x}^{2}-3x+6}{x+2}$-$\frac{x+2}{x+2}$)÷$\frac{(x+2)(x-2)}{{(x+2)}^{2}}$
=$\frac{{x}^{2}-4x+4}{x+2}$×$\frac{x+2}{x-2}$
=$\frac{{(x-2)}^{2}}{x-2}$
=x-2
当x=2+$\sqrt{5}$时,
原式=2+$\sqrt{5}$-2=$\sqrt{5}$.
点评 此题主要考查了分式的化简求值问题,要熟练掌握,解答此题的关键是要明确:在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
14.下列调查中,调查方式选择合理的是( )
| A. | 为了了解某一品牌家具的甲醛含量,选择全面调查 | |
| B. | 为了了解某公园全年的游客流量,选择抽样调查 | |
| C. | 为了了解神舟飞船的设备零件的质量情况,选择抽样调查 | |
| D. | 为了了解一批袋装食品是否含有防腐剂,选择全面调查 |
4.下列各数:3.414,-$\frac{22}{7}$,$\sqrt{8}$,π,4.$\stackrel{•}{2}$$\stackrel{•}{1}$$\stackrel{•}{7}$,0.1010010001…,其中无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.甲、乙两人进行射击练习,两人在相同条件下各射靶5次,射击成绩统计如下:
则甲、乙两人射击成绩的平均数分别是 (单位:环)( )
| 命中环数(单位:环) | 7 | 8 | 9 | 10 |
| 甲命中相应环数的次数 | 2 | 2 | 0 | 1 |
| 乙命中相应环数的次数 | 1 | 3 | 1 | 0 |
| A. | 5、5 | B. | 40、40 | C. | 8、8 | D. | 25、24 |
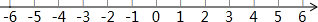 解不等式组$\left\{\begin{array}{l}{x+1≤3}\\{x-1<4(x+2)}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{x+1≤3}\\{x-1<4(x+2)}\end{array}\right.$,并把解集在数轴上表示出来. 已知:如图,在平面直角坐标系xOy中,直线y=$\frac{4}{3}$x+4与x轴交于A、与y轴交于 B,点C(a,b),其中a<b,且a、b是方程x2-7x+12=0的两根.
已知:如图,在平面直角坐标系xOy中,直线y=$\frac{4}{3}$x+4与x轴交于A、与y轴交于 B,点C(a,b),其中a<b,且a、b是方程x2-7x+12=0的两根.