题目内容
如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=![]() 30°.
30°.
(1)试判断直线CD与⊙O的位置关系,并说明理由.
(2)若⊙O的半径长为1,求由![]() 、线段BD和CD围成的阴影部分的面积(结果保留π和根号).
、线段BD和CD围成的阴影部分的面积(结果保留π和根号).
 |
(1)CD与⊙O相切
理由:∵∠BOC=2∠A=60°
又OC=OB
∴△为等边△(3′)
∴∠OCB=60°
∵∠BCD=30°
∴∠OCD=90°
∴CD与⊙O相切(5′)
(2)解:在△OCD中,∠OCD=90°
∵∠COB=60°
∴∠D=30°
∴OD=2OC=2
∴![]()
∴![]() (7′)
(7′)
 (10′)
(10′)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图△ABC内接于⊙O,PA,PB是⊙O的两条切线,已知AC=BC,∠ABC=2∠P,则∠ACB的弧度数为( )
如图△ABC内接于⊙O,PA,PB是⊙O的两条切线,已知AC=BC,∠ABC=2∠P,则∠ACB的弧度数为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,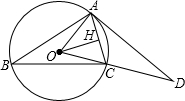 已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=
 如图△ABC内接于圆O,I是△ABC的内心,AI的延长线交圆O于点D.
如图△ABC内接于圆O,I是△ABC的内心,AI的延长线交圆O于点D. 已知:如图∠ABC内接于⊙O,BD⊥半径OA于D.BD=4.8,sinC=
已知:如图∠ABC内接于⊙O,BD⊥半径OA于D.BD=4.8,sinC=