题目内容
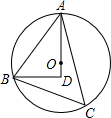 已知:如图∠ABC内接于⊙O,BD⊥半径OA于D.BD=4.8,sinC=
已知:如图∠ABC内接于⊙O,BD⊥半径OA于D.BD=4.8,sinC=| 4 | 5 |
5
5
.分析:过点O作OE⊥AB于点E,由垂径定理可知AE=
AB,∠AOE=∠C,设OA=r,则OE=3r,AE=4r,AB=8r,再由相似三角形的判定定理可得出Rt△AOE∽Rt△ABD,根据相似三角形的对应边成比例即可得出结论.
| 1 |
| 2 |
解答: 解:过点O作OE⊥AB于点E,则AE=
解:过点O作OE⊥AB于点E,则AE=
AB,∠AOE=∠C,设OA=r,则OE=3r,AE=4r,AB=8r,
∵OE⊥AB,BD⊥半径OA于D,
∴∠AEO=∠ADB=90°,∠BAD=∠BAD,
∴Rt△AOE∽Rt△ABD,
∴
=
,即
=
,
∴r=5.
故答案为:5.
 解:过点O作OE⊥AB于点E,则AE=
解:过点O作OE⊥AB于点E,则AE=| 1 |
| 2 |
∵OE⊥AB,BD⊥半径OA于D,
∴∠AEO=∠ADB=90°,∠BAD=∠BAD,
∴Rt△AOE∽Rt△ABD,
∴
| OA |
| AB |
| OE |
| BD |
| r |
| 8r |
| 3r |
| 4.8 |
∴r=5.
故答案为:5.
点评:本题考查的是圆周角定理及垂径定理,相似三角形的判定与性质,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,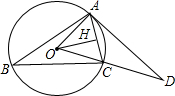
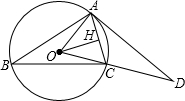 已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=
 已知:如图△ABC内接于⊙0,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q,下列结论:①∠ABC=∠DBC;②PD=PE:③P是△ACQ的外心;④
已知:如图△ABC内接于⊙0,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q,下列结论:①∠ABC=∠DBC;②PD=PE:③P是△ACQ的外心;④