��Ŀ����
12����ͼ��������y=$\frac{1}{2}$��x-3��2-1��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C������ΪD����1�����A��B��D�����ꣻ
��2������CD����ԭ��O��OE��CD������ΪH��OE�������ߵĶԳ��ύ�ڵ�E������AE��AD����֤����AED=��DAB��
��3���ԣ�2���еĵ�EΪԲ�ģ�1.5Ϊ�뾶��Բ���ڶԳ����Ҳ������������һ����P������P����E�����ߣ��е�ΪQ����PQ�ij���Сʱ�����P�����꣬��д����PAB������ֵ��
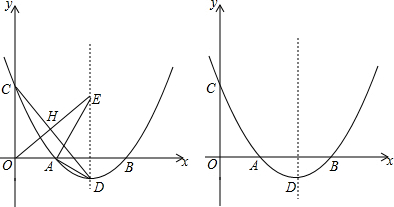
���� ��1����y=0���õ�$\frac{1}{2}$��x-3��2-1=0���ⷽ�̼������A��B�����ֱ꣬�Ӹ��ݽ���ʽ�Ķ���ʽ���D������ꣻ
��2����D��DG��y�ᣬ����ΪG����G��0��-1����GD=3�����C������꣬���CG=$\frac{9}{2}$��ͨ��֤�á�DCG�ס�EOM��Ӧ�߳ɱ������EM=2���Ӷ����ED=3��E��3��2��Ȼ���ݹ��ɶ������涨��֤�á�AED��ֱ�������Σ�����֤�ý��ۣ�
��3�����ݹ��ɶ����Լ����ߵ����ʣ����ڰ뾶�Ƕ�ֵ��֪��Ҫʹ���߳���С��ֻ��EP����С����P������Ϊ��x��$\frac{1}{2}$��x-3��2-1�������ݹ��ɶ������EP2=��x-3��2+[$\frac{1}{2}$��x-3��2-1-2]2���裨x-3��2=z�����û�Ԫ���ó�EP2=$\frac{1}{4}$��z-4��2+5��������x-3��2=4ʱ��EP2ȡ����СֵΪ5�����ݣ�x-3��2=4�����x��ֵ�������������P�����꣮
��� �⣺��1����y=$\frac{1}{2}$��x-3��2-1�У���y=0����$\frac{1}{2}$��x-3��2-1=0����ã�x1=3-$\sqrt{2}$��x2=3+$\sqrt{2}$��
��A��3-$\sqrt{2}$��0����B��3+$\sqrt{2}$��0����
�������ߵĶ���ʽ��֪D��3��-1����
��2����ͼ1����D��DG��y�ᣬ����ΪG����G��0��-1����GD=3��
��������y=$\frac{1}{2}$��x-3��2-1��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
���x=0����ã�y=$\frac{7}{2}$��
��GC=$\frac{9}{2}$��
��Գ��ύx���ڵ�M��
��OE��CD����BOC=90�㣬
���DCO=��EOM��
�ߡ�OME=��CGD=90�㣬
���DCG�ס�EOM��
��$\frac{CG}{OM}$=$\frac{DG}{EM}$����$\frac{\frac{9}{2}}{3}$=$\frac{3}{EM}$��
��EM=2��
��ED=3��E��3��2����
��AE2=��3-$\sqrt{2}$-3��2+22=6��AD2=��3-$\sqrt{2}$-3��2+12=3��ED2=32=9��
��AE2+AD2=ED2��
���AED��ֱ�������Σ�
���AED+��ADE=90�㣬
�ߡ�DAB+��ADE=90�㣬
���AED=��DAB��
��3����ͼ2����P������Ϊ��x��$\frac{1}{2}$��x-3��2-1����Ҫʹ���߳���С��ֻ��EP����С��
��E��3��2����
��EP2=��x-3��2+[$\frac{1}{2}$��x-3��2-1-2]2��
�裨x-3��2=z��
��EP2=$\frac{1}{4}$��z-4��2+5��
�൱��x-3��2=4ʱ��EP2ȡ����СֵΪ5��
�ߣ�x-3��2=4��
��x1=5��x2=1����ȥ����
���P��������5��1����
��tan��PAB=$\frac{1}{5-��3-\sqrt{2}��}$=$\frac{1}{2+\sqrt{2}}$=$\frac{2-\sqrt{2}}{2}$��
���� �����Ƕ��κ������ۺ��⣬�����˶��κ��������ʣ����κ���ͼ���ϵ���������������������Ƶ��ж������ʣ����ɶ�����Ӧ�ã����ߵ������Լ���������ֵ�ȣ������������ʶ����ǽ���Ĺؼ���

 ����������������ϵ�д�
����������������ϵ�д�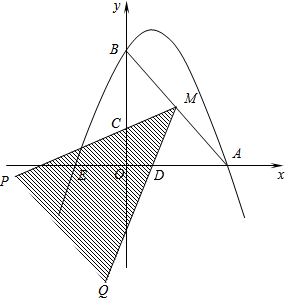 ��֪������y=-$\frac{1}{2}$x2+bx+4��x���y���������ֱ��ڵ�A��B����֪B������Ϊ��4��0����
��֪������y=-$\frac{1}{2}$x2+bx+4��x���y���������ֱ��ڵ�A��B����֪B������Ϊ��4��0����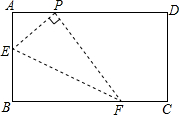 ��ͼ���ھ���ABCD�У���P��AD�ϣ�AB=2��AP=1��E��AB�ϵ�һ�����㣬����PE������P��PE�Ĵ��ߣ���BC�ڵ�F������EF����EF���е�ΪG������E�ӵ�B�˶�����Aʱ����G�ƶ���·���ij���$\sqrt{5}$��
��ͼ���ھ���ABCD�У���P��AD�ϣ�AB=2��AP=1��E��AB�ϵ�һ�����㣬����PE������P��PE�Ĵ��ߣ���BC�ڵ�F������EF����EF���е�ΪG������E�ӵ�B�˶�����Aʱ����G�ƶ���·���ij���$\sqrt{5}$��
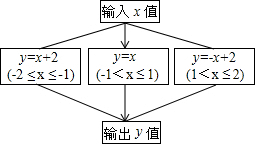 ������ͼ��ʾ�ij�����㺯��ֵ���������yֵΪ-0.5���������xֵΪ-0.5��
������ͼ��ʾ�ij�����㺯��ֵ���������yֵΪ-0.5���������xֵΪ-0.5��