题目内容
 已知AB、CD相交于点O,AC∥DB,OC=OD,EF为OC上的两个点,且AE=BF,求证:CE∥DF.
已知AB、CD相交于点O,AC∥DB,OC=OD,EF为OC上的两个点,且AE=BF,求证:CE∥DF.考点:全等三角形的判定与性质,平行线的判定与性质
专题:证明题
分析:由AC与DB平行,利用两直线平行内错角相等得到两对角相等,再由OC=OD,利用AAS得到三角形AOC与三角形BOD全等,利用确定三角形对应边相等得到OA=OB,根据AE=BF得到OE=OF,利用SAS得到三角形EOC与三角形FOD全等,利用全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答:证明:∵AC∥DB,
∴∠A=∠B,∠ACO=∠BDO,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(AAS),
∴OA=OB,
∵AE=BF,
∴OA-AE=OB-FB,即OE=OF,
在△EOC和△FOD中,
,
∴△EOC≌△FOD(SAS),
∴∠CEO=∠DFO,
∴CE∥DF.
∴∠A=∠B,∠ACO=∠BDO,
在△AOC和△BOD中,
|
∴△AOC≌△BOD(AAS),
∴OA=OB,
∵AE=BF,
∴OA-AE=OB-FB,即OE=OF,
在△EOC和△FOD中,
|
∴△EOC≌△FOD(SAS),
∴∠CEO=∠DFO,
∴CE∥DF.
点评:此题考查了全等三角形的判定与性质,平行线的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
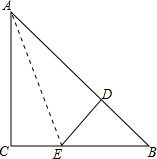 已知Rt△ABC中,∠ACB=90°,AC=BC,AD=AC,DE⊥AB,垂足为D,交BC于点E.求证:BD=DE=CE.
已知Rt△ABC中,∠ACB=90°,AC=BC,AD=AC,DE⊥AB,垂足为D,交BC于点E.求证:BD=DE=CE.