题目内容
如图,已知正比例函数和反比例函数的图象都经过点M(-2,-1),且P(-1,-2)为双曲线上的一点 ,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
(1)写出正比例函数和反比例函数的关系式;
(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标;如果不存在,请说明理由.
解:(1)设反比例函数的解析式为y= (k≠0),正比例函数的解析式为y=k′x.
(k≠0),正比例函数的解析式为y=k′x.
∵正比例函数和反比例函数的图象都经过点M(-2,-1),
∴-1=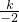 ,-1=-2k′,
,-1=-2k′,
∴k=2,k′= .
.
∴正比例函数的解析式为y= x,反比例函数的解析式为y=
x,反比例函数的解析式为y= .
.
(2)当点Q在直线MO上运动时,假设在直线MO上存在这样的点Q(x, x),使得△OBQ与△OAP面积相等,则B(0,
x),使得△OBQ与△OAP面积相等,则B(0, x).
x).
∵S△OBQ=S△OAP,
∴ •x
•x x=
x= ×2×1,
×2×1,
解得x=±2.
当x=2时, x=1;
x=1;
当x=-2时, x=-1.
x=-1.
故在直线MO上存在这样的点Q(2,1)或(-2,-1),使得△OBQ与△OAP面积相等.
分析:(1)设反比例函数的解析式为y= ,正比例函数的解析式为y=k′x.把点M(-2,-1)分别代入其函数解析式,运用待定系数法即可求出对应的函数的关系式;
,正比例函数的解析式为y=k′x.把点M(-2,-1)分别代入其函数解析式,运用待定系数法即可求出对应的函数的关系式;
(2)当点Q在直线MO上运动时,假设在直线MO上存在这样的点Q(x, x),使得△OBQ与△OAP面积相等,则B(0,
x),使得△OBQ与△OAP面积相等,则B(0, x).根据三角形的面积公式列出关于x的方程,解方程即可.
x).根据三角形的面积公式列出关于x的方程,解方程即可.
点评:本题考查了运用待定系数法求函数的解析式及三角形的面积,利用形数结合解决此类问题,是非常有效的方法.
 (k≠0),正比例函数的解析式为y=k′x.
(k≠0),正比例函数的解析式为y=k′x.∵正比例函数和反比例函数的图象都经过点M(-2,-1),
∴-1=
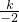 ,-1=-2k′,
,-1=-2k′,∴k=2,k′=
 .
.∴正比例函数的解析式为y=
 x,反比例函数的解析式为y=
x,反比例函数的解析式为y= .
.(2)当点Q在直线MO上运动时,假设在直线MO上存在这样的点Q(x,
 x),使得△OBQ与△OAP面积相等,则B(0,
x),使得△OBQ与△OAP面积相等,则B(0, x).
x).∵S△OBQ=S△OAP,
∴
 •x
•x x=
x= ×2×1,
×2×1,解得x=±2.
当x=2时,
 x=1;
x=1;当x=-2时,
 x=-1.
x=-1.故在直线MO上存在这样的点Q(2,1)或(-2,-1),使得△OBQ与△OAP面积相等.
分析:(1)设反比例函数的解析式为y=
 ,正比例函数的解析式为y=k′x.把点M(-2,-1)分别代入其函数解析式,运用待定系数法即可求出对应的函数的关系式;
,正比例函数的解析式为y=k′x.把点M(-2,-1)分别代入其函数解析式,运用待定系数法即可求出对应的函数的关系式;(2)当点Q在直线MO上运动时,假设在直线MO上存在这样的点Q(x,
 x),使得△OBQ与△OAP面积相等,则B(0,
x),使得△OBQ与△OAP面积相等,则B(0, x).根据三角形的面积公式列出关于x的方程,解方程即可.
x).根据三角形的面积公式列出关于x的方程,解方程即可.点评:本题考查了运用待定系数法求函数的解析式及三角形的面积,利用形数结合解决此类问题,是非常有效的方法.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 边形OABD的面积S满足:S1=
边形OABD的面积S满足:S1=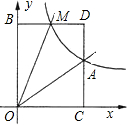 如图,已知正比例函数y=ax与反比例函数y=
如图,已知正比例函数y=ax与反比例函数y=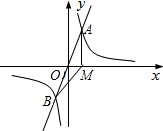 标为1,过点A作x轴的垂线,垂足为M,连接BM.
标为1,过点A作x轴的垂线,垂足为M,连接BM. 如图,已知正比例函数y=kx的图象经过点A(-
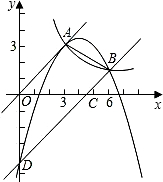
如图,已知正比例函数y=kx的图象经过点A(- 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).