题目内容
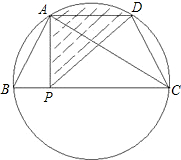 如图,梯形ABCD的四个顶点均在已知圆上,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为20,P是BC上一点,则阴影部分的面积等于________.
如图,梯形ABCD的四个顶点均在已知圆上,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为20,P是BC上一点,则阴影部分的面积等于________.
 π
π分析:首先根据∠ADC的度数求出∠ACD、∠ACB、∠ABC的度数;然后证明∠BAC=90°,得出BC是梯形外接圆的直径,设圆心为0,连接OA、OD,由于△OAD和△APD同底等高,故阴影部分的面积是扇形OAD的面积.扇形圆心角的度数可由圆周角定理求得,关键是求出扇形的半径;可在Rt△ABC中求出BC与AB的关系,进一步根据梯形的周长求出⊙O的直径,由此得解.
解答:
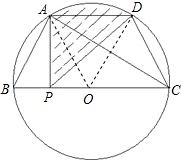 解:如图,设梯形ABCD的外接圆圆心为O,连接OA、OD;
解:如图,设梯形ABCD的外接圆圆心为O,连接OA、OD;∵AD∥BC,
∴∠BCD=180°-∠ADC=60°;
∵AC平分∠BCD,
∴∠ACD=∠ACB=30°;
∵∠ADC=120°,
∴∠BCD=60°,
∴∠ABC=∠BCD=60°,
∴四边形ABCD是等腰梯形,
∴∠ABC=DCB=60°;
∴∠BAC=90°;
即BC是⊙O的直径;
Rt△ABC中,∠ACB=30°,BC=2AB;
△ACD中,∠ADC=120°,∠ACD=30°;
∴∠CAD=∠ACD=30°,即AD=CD=AB=
 BC;
BC;∵梯形ABCD的周长为20
∴AB+AD+CD+BC=
 BC=20,即BC=8;
BC=20,即BC=8;∴OA=OD=4;
又∵∠AOD=2∠ACD=60°,
∴S扇形AOD=
 =
=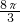 ;
;∵△APD与△AOD同底等高,
∴S△APD=S△AOD;
∴S阴影=S△APD+S弓形AD=S△AOD+S弓形AD=S扇形AOD=
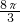 .
.点评:此题主要考查了梯形的性质、圆周角定理以及扇形面积的计算方法,难点在于确定BC是梯形外接圆的直径.

练习册系列答案
相关题目
 如图,梯形ABCD的对角线交于点O,有以下四个结论:
如图,梯形ABCD的对角线交于点O,有以下四个结论:①△AOB∽△COD,②△AOD∽△ACB,③S△DOC:S△AOD=DC:AB,④S△AOD=S△BOC,其中始终正确的有( )个.
| A、1 | B、2 | C、3 | D、4 |
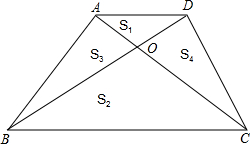 如图,梯形ABCD的对角线AC、BD相交于点O,△ADO的面积记作S1,△BCO的面积记作S2,△ABO的面积记作S3,△CDO的面积记作S4,则下列关系正确是( )
如图,梯形ABCD的对角线AC、BD相交于点O,△ADO的面积记作S1,△BCO的面积记作S2,△ABO的面积记作S3,△CDO的面积记作S4,则下列关系正确是( )| A、S1=S2 | B、S1×S2=S3×S4 | C、S1+S2=S4+S3 | D、S2=2S3 |
 14、如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
14、如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
 16、如图,梯形ABCD的对角线交于点O,有以下三个结论:
16、如图,梯形ABCD的对角线交于点O,有以下三个结论: 如图,梯形ABCD的面积为34cm2,AE=BF,CE与DF相交于O,△OCD的面积为11cm2,则阴影部分的面积为
如图,梯形ABCD的面积为34cm2,AE=BF,CE与DF相交于O,△OCD的面积为11cm2,则阴影部分的面积为