题目内容
6.若$\sqrt{n-3}$+|m-1|=0且一元二次方程kx2+nx+m=0有两个实数根,则k的取值范围是k≤$\frac{9}{4}$,且k≠0.分析 首先利用非负数的性质得出m=1,n=3,得出方程kx2+3x+1=0,则根的判别式△=b2-4ac≥0,建立关于k的不等式,求出k的取值范围.还要注意二次项系数不为0.
解答 解:∵$\sqrt{n-3}$+|m-1|=0,
∴m=1,n=3,
∴方程kx2+3x+1=0,
∴△=32-4k=9-4k≥0,且k≠0,
解得:k≤$\frac{9}{4}$,且k≠0.
故答案为:k≤$\frac{9}{4}$,且k≠0.
点评 此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知△ABC≌△DEF,且∠A=60°,∠E=50°,则∠F等于( )
| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
 如图,a,b为数轴上的两点表示的有理数,在a+b,b-a,|a-b|,|b|-|a|中,负数的个数有( )
如图,a,b为数轴上的两点表示的有理数,在a+b,b-a,|a-b|,|b|-|a|中,负数的个数有( ) 如图,长方体的长AB=10,宽BC=5,高为8,点B处有一只蚂蚁,点N处有一滴蜂蜜,如果蚂蚁要沿着长方体的表面从点B爬到点N,需要爬行的最短距离是$\sqrt{269}$.
如图,长方体的长AB=10,宽BC=5,高为8,点B处有一只蚂蚁,点N处有一滴蜂蜜,如果蚂蚁要沿着长方体的表面从点B爬到点N,需要爬行的最短距离是$\sqrt{269}$.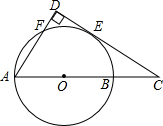 如图,O为Rt△ACD的斜边AC上一点,以O为圆心,OA为半径的圆与DC相切于点E,分别交AC、AD于点B和点F.若⊙O的半径为3cm,DF=1cm,则DE的长是$\sqrt{5}$cm.
如图,O为Rt△ACD的斜边AC上一点,以O为圆心,OA为半径的圆与DC相切于点E,分别交AC、AD于点B和点F.若⊙O的半径为3cm,DF=1cm,则DE的长是$\sqrt{5}$cm.