题目内容
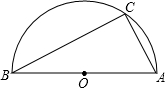
如图,AB为半圆O的直径,延长AB到点P,使BP= AB,PC切半圆O于点C,点D是
AB,PC切半圆O于点C,点D是 上和点C不重合的一点,则∠CDB的度数为 度.
上和点C不重合的一点,则∠CDB的度数为 度.
【答案】分析:连接OC,由切线的性质得OC⊥PC,于是易得Rt△OCP中,OC=OB=PB;利用30°所对的边等于斜边的一半,可得∠P=30°,于是得∠COP=60°,再由“同弧所对的圆周角等于它所对的圆心角的一半”得∠CDB=30度.
解答: 解:连接OC,
解:连接OC,
∵PC切半圆O于点C,
∴OC⊥PC,
∴OC=OB=PB,
∴∠P=30°,即∠COP=60°,
∴∠CDB= ∠COP=30°.
∠COP=30°.
点评:本题考查了直角三角形中30°角的确定及圆周角与圆心角的关系,属综合性稍强的题目,学生由于应用中的某一类知识欠缺导致出现错误.
解答:
 解:连接OC,
解:连接OC,∵PC切半圆O于点C,
∴OC⊥PC,
∴OC=OB=PB,
∴∠P=30°,即∠COP=60°,
∴∠CDB=
 ∠COP=30°.
∠COP=30°.点评:本题考查了直角三角形中30°角的确定及圆周角与圆心角的关系,属综合性稍强的题目,学生由于应用中的某一类知识欠缺导致出现错误.

练习册系列答案
相关题目
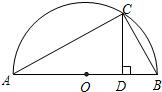 为D,AD=a,DB=b.
为D,AD=a,DB=b.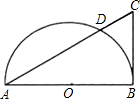 如图,AB为半圆O的直径,CB切半圆于点B,AC交半圆于点D,若CD=1,AD=3,则⊙O半径的长为
如图,AB为半圆O的直径,CB切半圆于点B,AC交半圆于点D,若CD=1,AD=3,则⊙O半径的长为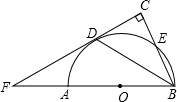 C,直线CD交BA的延长线于点F.
C,直线CD交BA的延长线于点F. 如图,AB为半圆O的直径,B1,B2,…,Bk是半圆上的k个点,满足BB1=B1B2=…Bk-1Bk,对于线段OB1,OB2,…,OBk,AB1,AB2,…,ABk,当k=4时,有
如图,AB为半圆O的直径,B1,B2,…,Bk是半圆上的k个点,满足BB1=B1B2=…Bk-1Bk,对于线段OB1,OB2,…,OBk,AB1,AB2,…,ABk,当k=4时,有