Question

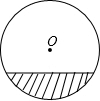
一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽0.8米，最深处水深0.2米，则此输水管道的半径是      米．

Answer 1

0.5

解析试题分析：设⊙O的半径是R，过点O作OD⊥AB于点D，交⊙O于点C，连接OA，由垂径定理得出AD的长，在Rt△AOD中利用勾股定理即可求出OA的长．
设⊙O的半径是R，过点O作OD⊥AB于点D，交⊙O于点C，连接OA，

∵AB=0.8m，OD⊥AB，
∴AD=0.4m，
∵CD=0.2m，
∴OD=R-CD=R-0.2，
在Rt△OAD中，，
即，
解得R=0.5m，
则此输水管道的半径是0.5米．
考点：本题考查的是垂径定理，勾股定理
点评：解答本题的关键是根据题意作出辅助线，构造直角三角形。