题目内容
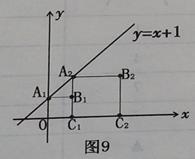
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.
(1)从运动开始,当t取何值时,PQ∥CD?
(2)从运动开始,当t取何值时,△PQC为直角三角形?
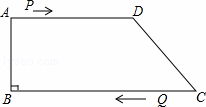
解:(1)当PQ∥CD时,四边形PDCB是平行四边形,
此时PD=QC,
∴12﹣2t=t,
∴t=4.
∴当t=4时,四边形PQDC是平行四边形.
(2)过P点,作PE⊥BC于E,DF⊥BC,
∴DF=AB=8.
FC=BC﹣AD=18﹣12=6.
①当P Q⊥BC,
Q⊥BC,
则BE+CE=18.即:2t+t=18 ,
,
∴t=6;
②当QP⊥PC,
∴PE=4,CE=3+t,QE=12﹣2t﹣(3+t)=9﹣3t,
∴16=(3+t)(9﹣3t),
解得:t= ,
,
③情形:当PC⊥BC时,因∠DCB<90°,此种情形不存在.
∴当t=3或 时,△PQC是直角三角形.
时,△PQC是直角三角形.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 B.
B.  C.
C.  D.
D. 
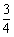 ,求DC的长.
,求DC的长.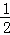 GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
 +
+ .
.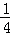 =(x﹣
=(x﹣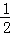 )2
)2