题目内容
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=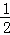 GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
B. 解:∵四边形ABCD是正方形,
∴∠B=∠DCB=90°,AB=BC,
∵AG=CE,
∴BG=BE,
由勾股定理得:BE= GE,∴①错误;
GE,∴①错误;
∵BG=BE,∠B=90°,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∴∠GAE+∠AEG=45°,
∵AE⊥EF,
∴∠AEF=90°,
∵∠BEG=45°,
∴∠AEG+∠FEC=45°,
∴∠GAE=∠FEC,
在△GAE和△CEF中

∴△GAE≌△CEF,∴②正确;
∴∠AGE=∠ECF=135°,
∴∠FCD=135°﹣90°=45°,∴③正确;
∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,
∴∠FEC<45°,
∴△GBE和△ECH不相似,∴④错误;
即正确的有2个.

练习册系列答案
相关题目
 ,
, 这四个数中,最大的数是
这四个数中,最大的数是 的中点P作⊙O的直径PG交弦BC于点D,连接AG, CP,PB.
的中点P作⊙O的直径PG交弦BC于点D,连接AG, CP,PB.
 的解集中共有5个整数,则a的取值范围为( )
的解集中共有5个整数,则a的取值范围为( ) 等的正方形、长方形、圆,这三个几何图形中,圆面积最大
等的正方形、长方形、圆,这三个几何图形中,圆面积最大