题目内容
 如图所示,是一个自然数排列的三角形数阵:根据该数阵的规律,第6行第3个数是
如图所示,是一个自然数排列的三角形数阵:根据该数阵的规律,第6行第3个数是18
18
,第n行第2个数是| n2-n+4 |
| 2 |
| n2-n+4 |
| 2 |
分析:观察数据得到第一行有1个数,第二行有2个数,…,即每行的数字的个数等于此行的行数,则第五行最后一个数为1+2+3+4+5=15,再加数三个数得到第6行第3个数;
由于第(n-1)行有(n-1)个数,则第n-1行最后一个数为1+2+3+4+5+…+n-1=
,然后再加两个数即可得到第n行第2个数.
由于第(n-1)行有(n-1)个数,则第n-1行最后一个数为1+2+3+4+5+…+n-1=
| n(n-1) |
| 2 |
解答:解:第一行有1个数,
第二行有2个数,
第三行有3个数,
第四行有4个数,
第五行有5个数,则第五行最后一个数为1+2+3+4+5=15,
所以第六行有6个数,其中第一个数为16,第二个数为17,第三个数为18,
…
第(n-1)行有(n-1)个数,则第n-1行最后一个数为1+2+3+4+5+…+n-1=
,
所以第n行第一个数为
+1,第二个数为
+2=
.
故答案为18,
.
第二行有2个数,
第三行有3个数,
第四行有4个数,
第五行有5个数,则第五行最后一个数为1+2+3+4+5=15,
所以第六行有6个数,其中第一个数为16,第二个数为17,第三个数为18,
…
第(n-1)行有(n-1)个数,则第n-1行最后一个数为1+2+3+4+5+…+n-1=
| n(n-1) |
| 2 |
所以第n行第一个数为
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
| n2-n+4 |
| 2 |
故答案为18,
| n2-n+4 |
| 2 |
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
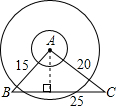
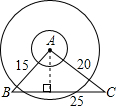 如图所示,已知B、C两个乡镇相距25千米,有一个自然保护区A与B相距15千米,与C相距20千米,以点A为圆心,10千米为半径是自然保护区的范围,现在要在B、C两个乡镇之间修一条笔直的公路,请问:这条公路是否会穿过自然保护区?试通过计算加以说明.
如图所示,已知B、C两个乡镇相距25千米,有一个自然保护区A与B相距15千米,与C相距20千米,以点A为圆心,10千米为半径是自然保护区的范围,现在要在B、C两个乡镇之间修一条笔直的公路,请问:这条公路是否会穿过自然保护区?试通过计算加以说明.
 如图所示,已知B、C两个乡镇相距25千米,有一个自然保护区A与B相距15千米,与C相距20千米,以点A为圆心,10千米为半径是自然保护区的范围,现在要在B、C两个乡镇之间修一条笔直的公路,请问:这条公路是否会穿过自然保护区?试通过计算加以说明.
如图所示,已知B、C两个乡镇相距25千米,有一个自然保护区A与B相距15千米,与C相距20千米,以点A为圆心,10千米为半径是自然保护区的范围,现在要在B、C两个乡镇之间修一条笔直的公路,请问:这条公路是否会穿过自然保护区?试通过计算加以说明.