题目内容
如图,正方形ABCD的边长为3,将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°),得到正方形AEFG,FE交线段DC于点Q,FE的延长线交线段BC于点P,连结AP、AQ.
(1)求证:△ADQ≌△AEQ;
(2)求证:PQ=DQ+PB;
(3)当∠1=∠2时,求PQ的长.(杭十五中模拟)
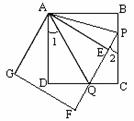
(1)∵ABCD是正方形,∴在Rt△ADQ和Rt△AEQ中,
有AD=AE,AQ=AQ, ∴△ADQ≌△AEQ(HL)
 (2)同理可证得△AEP≌△ABP-
(2)同理可证得△AEP≌△ABP-
∴PB=PE,由(1)QD=QE,∴PQ=QE+PE=DQ+PB-
(3)当∠1=∠2时,Rt△ADQ∽Rt△PCQ,∴∠3=∠4,又∵∠3=∠5
∴∠3=∠4=∠5,且∠3+∠4+∠5=180°,∴∠3=60° --------------1分
∴Rt△ADQ中,AD=3,DQ=
∴QC=3— ,∴PQ=2QC= 6—2
,∴PQ=2QC= 6—2

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
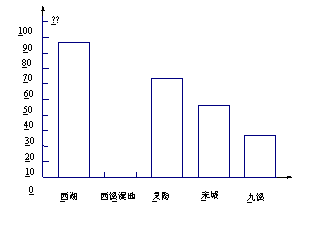
杭州是一座美丽的旅游城市,吸引了很多的国内外游客,某旅行社对11月份本社接待的外地游客来杭州旅游的首选景点作了一次抽样调查. 调查结果如下图表:
 | ||||||||||||||||||||
| ||||||||||||||||||||
(1)此次共调查了多少人?
(2)请将以上图表补充完整.
(3)该旅行社预计12月份接待外地来杭的游客2500人,请你估计首选去西湖的人数约有多少人.
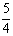 B.1 C.
B.1 C.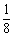 D. 不存在
D. 不存在

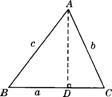 在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作  ,sinC=
,sinC= ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即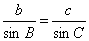 .同理有:
.同理有: ,
, ,
,