题目内容
如图，已知矩形ABCD中，ABEF是正方形，且矩形CDFE与矩形ABCD相似，求矩形ABCD的宽与长的比．
解：∵矩形CDFE与矩形ABCD相似，
∴
=
，
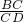∴CD2=BC×CE=BC（BC-CD），
即AB2=AD×（AD-AB），
∴AB2+AB•AD-AD2=0，
方程两边同除以AD2得：（
）2+-1=0
解得：=
． …（8分）
分析：利用相似多边形的对应边的比等于相似比及正方形的性质进行计算即可．
点评：此题主要考查了相似多边形的对应边的比相等，注意分清对应边是解决本题的关键．
∴
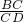=，∴CD2=BC×CE=BC（BC-CD），
即AB2=AD×（AD-AB），
∴AB2+AB•AD-AD2=0，
方程两边同除以AD2得：（
）2+-1=0解得：
=． …（8分）分析：利用相似多边形的对应边的比等于相似比及正方形的性质进行计算即可．
点评：此题主要考查了相似多边形的对应边的比相等，注意分清对应边是解决本题的关键．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
如图，已知矩形DEFG内接于Rt△ABC，D在AB上，E、F在BC上，G在AC上，∠BAC=90°，AB=6cm，AC=8cm，
m/秒的速度移动，如果M、N两点同时出发，移动的时间为x秒（0≤x≤6）．
点A运动．
（2012•宁德质检）如图，已知Rt△ABC，∠B=90°，AB=8，BC=6，把斜边AC平均分成n段，以每段为对角线作边与AB、BC平行的小矩形，则这些小矩形的面积和是（ ）
如图，已知矩形ABCD中AB：BC=3：1，点A、B在x轴上，直线y=mx+n（0＜m＜n＜