题目内容
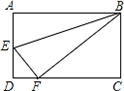
 如图,已知矩形DEFG内接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm,S矩形DEFG=
如图,已知矩形DEFG内接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm,S矩形DEFG=| 45 | 4 |
分析:作辅助线,作AM⊥BC于M,交DG于N,根据△ADG∽△ABC得出对应边成比例,再设DE=x,根据矩形面积得DG,又因为∠BAC=90°,AB=6cm,AC=8cm,求得AM,再将①式化简即可.
解答: 解:如图,作AM⊥BC于M,交DG于N,
解:如图,作AM⊥BC于M,交DG于N,
在矩形DEFG中,DG∥BC,
∴△ADG∽△ABC,
∴
=
①,
设DE=x,
∵S矩DEFG=DE•DG=
,
∴DG=
cm,
又∵∠BAC=90°,AB=6cm,AC=8cm,
∴BC=
=10cm,
∵S△ABC=
BC•AM=
AB•AC,
∴AM=
=
,
AN=AM-x=
-x,
∴①式可化为
=
,
∴5x2-24x+27=0,解得x1=3,x2=1
,
∴DE长为3cm或1
cm,
当DE=3cm时,DG=3
cm,
当DG=
cm时,DG=6
cm.
故答案为:3
或6
cm.
 解:如图,作AM⊥BC于M,交DG于N,
解:如图,作AM⊥BC于M,交DG于N,在矩形DEFG中,DG∥BC,
∴△ADG∽△ABC,
∴
| AN |
| AM |
| DG |
| BC |
设DE=x,
∵S矩DEFG=DE•DG=
| 45 |
| 4 |
∴DG=
| 45 |
| 4x |
又∵∠BAC=90°,AB=6cm,AC=8cm,
∴BC=
| AB2+AC2 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AM=
| AB•AC |
| BC |
| 24 |
| 5 |
AN=AM-x=
| 24 |
| 5 |
∴①式可化为
| ||
|
| ||
| 10 |
∴5x2-24x+27=0,解得x1=3,x2=1
| 4 |
| 5 |
∴DE长为3cm或1
| 4 |
| 5 |
当DE=3cm时,DG=3
| 3 |
| 4 |
当DG=
| 9 |
| 5 |
| 1 |
| 4 |
故答案为:3
| 3 |
| 4 |
| 1 |
| 4 |
点评:此题涉及到的知识点较多,有相似三角形的判定与性质,平行线的性质,三角形的面积.勾股定理,矩形的性质等,综合性较强,有一定的难度,是一道难题.

练习册系列答案
相关题目
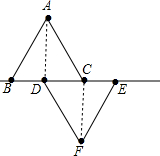 上,连接AD及CF.
上,连接AD及CF.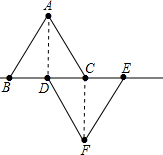 ,连接AD、CF.
,连接AD、CF.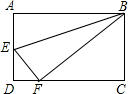 如图,已知矩形ABCD,E为AD上一点,F为CD上一点,若将矩形沿BE折叠,点A恰与点F重合,且△DEF为等腰三角形,DE=1,求矩形ABCD的面积.
如图,已知矩形ABCD,E为AD上一点,F为CD上一点,若将矩形沿BE折叠,点A恰与点F重合,且△DEF为等腰三角形,DE=1,求矩形ABCD的面积. 如图,已知矩形ABCD,E为AD上一点,F为CD上一点,若将矩形沿BE折叠,点A恰与点F重合,且△DEF为等腰三角形,DE=1,求矩形ABCD的面积.
如图,已知矩形ABCD,E为AD上一点,F为CD上一点,若将矩形沿BE折叠,点A恰与点F重合,且△DEF为等腰三角形,DE=1,求矩形ABCD的面积.