题目内容
如图，已知三个等圆⊙A、⊙B、⊙C两两外切，半径r=10cm，求三圆间阴影部分的面积．考点：相切两圆的性质
专题：
分析：运用相切的性质证明△ABC为等边三角形，进而得到∠A=∠B=∠C=60°；将图中的三个扇形不重叠的放在一起，就构成了一个半径为10cm的半圆，借助圆的面积公式，即可解决问题．
解答：解：如图，∵三个等圆⊙A、⊙B、⊙C两两外切，且半径r=10cm，
∴AB=AC=BC=20cm，△ABC为等边三角形，∠A=∠B=∠C=60°；
∴将图中的三个扇形不重叠的放在一起，就构成了一个半径为
10cm的半圆，
∴三圆间阴影部分的面积=
π•102=50π（cm2）．
解：如图，∵三个等圆⊙A、⊙B、⊙C两两外切，且半径r=10cm，∴AB=AC=BC=20cm，△ABC为等边三角形，∠A=∠B=∠C=60°；
∴将图中的三个扇形不重叠的放在一起，就构成了一个半径为
10cm的半圆，
∴三圆间阴影部分的面积=
| 1 |
| 2 |
点评：该题主要考查了相切两圆的性质及其应用问题；解题的关键是利用相切的性质证明△ABC为等边三角形；对分析问题解决问题的能力提出了一定的要求．
练习册系列答案
相关题目
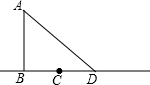如图，学校旗杆AB的顶端A处挂有一根绳子．小莹在测量旗杆的高度时，先把绳子沿旗杆下垂到点B，固定后再把余下的部分BC拉紧成线段BC（绳子的一端落在C点），然后再将绳子重新拉紧成线段AD（绳子的一端落在D点）．小莹只用卷尺在地面上测量了两个数据，就计算出了旗杆高度，你知道测量了哪两个数据吗？你能求出旗杆的高度吗？
如图，直线AD与AE相交于点A，直线BC分别交AD、AE于点B、C，直线DE分别交AD、AE于点D、E，分别写出图中的两对同位角、两对内错角、两对同旁内角．