ĖâÄŋÄÚČŨ
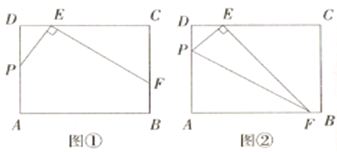
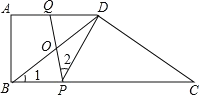
ĄžĖâÄŋĄŋČįÍŧŖŦÔÚABCDÖĐŖŦADĄÎBCŖŦĄĪA=90ĄãŖŦBD=DCŖŦAB=6ŖŦAD=8ŖŦĩãPĄĸQˇÖąđÎĒBCĄĸADÉĪĩÄļ¯ĩãŖŦÁŦŊĶPQŖŦĶëBDĪāŊģĶÚĩãOŖŽ
Ŗ¨1ŖŠĩąĄĪ1=ĄĪ2ĘąŖŦĮķÖ¤ŖēĄĪDOQ=ĄĪDPCŖģ
Ŗ¨2ŖŠĩąŖ¨1ŖŠĩÄĖõŧūĪÂŖŦĮķÖ¤ŖēDQĄ¤PC=BDĄ¤DOŖģ
Ŗ¨3ŖŠČįšûĩãPĶÉĩãBĪōĩãCŌÆļ¯ŖŦÃŋÃëŌÆļ¯2¸öĩĨÎģŖŦÍŦĘąĩãQĶÉĩãDĪōĩãAŌÆļ¯ŖŦÃŋÃëŌÆļ¯1¸öĩĨÎģŖŦÉčŌÆļ¯ĩÄĘąŧäÎĒtÃëŖŦĘĮˇņ´æÔÚÄŗŌģĘąŋĖŖŦĘšĩÃĄ÷BOPÎĒÖąŊĮČũŊĮĐÎŖŦČįšû´æÔÚŖŦĮëÖąŊĶĐ´ŗötĩÄÖĩŖģČįšû˛ģ´æÔÚŖŦĮëËĩÃ÷ĀíĶÉŖŽ
Ąž´đ°¸ĄŋŖ¨1ŖŠŧûĪęŊâŖģŖ¨2ŖŠŧûĪęŊâŖģŖ¨3ŖŠ´æÔÚŖģĩątŖŊ![]() ÃëģōtŖŊ
ÃëģōtŖŊ![]() ÃëĘąŖŦĄ÷BOPÎĒÖąŊĮČũŊĮĐÎŖŽ
ÃëĘąŖŦĄ÷BOPÎĒÖąŊĮČũŊĮĐÎŖŽ
ĄžŊâÎöĄŋ
Ŗ¨1ŖŠ¸ųžŨĪāËÆČũŊĮĐÎĩÄÅĐļ¨ļ¨ĀíÖ¤Ã÷Ą÷DOPĄ×Ą÷DPBŖŦĩÃĩŊĄĪDOP=ĄĪDPBŖŦ¸ųžŨÁÚ˛šŊĮĩÄ
ĐÔÖĘÖ¤Ã÷ŊáÂÛŖģ
Ŗ¨2ŖŠÖ¤Ã÷Ą÷DOQĄ×Ą÷CPDŖŦ¸ųžŨĪāËÆČũŊĮĐÎĩÄļÔĶĻąßŗÉąČĀũÖ¤Ã÷ŊáÂÛŖģ
Ŗ¨3ŖŠˇÖĸŲĄĪBPO=90ĄãēÍĸÚĄĪPOB=90ĄãÁŊÖÖĮéŋöŖŦ¸ųžŨžØĐÎĩÄĐÔÖĘēÍĪāËÆČũŊĮĐÎĩÄĐÔÖĘŧÆËãŧ´ŋÉŖŽ
Ŗ¨1ŖŠÖ¤Ã÷ŖēĄßĄĪPDO=ĄĪBDPŖŦĄĪ1=ĄĪ2ŖŦ
ĄāĄ÷DOPĄ×Ą÷DPBŖŦ
ĄāĄĪDOP=ĄĪDPBŖŦ
ĄßĄĪDOQ+ĄĪDOP=ĄĪDPC+ĄĪDPB=180ĄãŖŦ
ĄāĄĪDOQ=ĄĪDPCŖģ
Ŗ¨2ŖŠÖ¤Ã÷ŖēĄßADĄÎBCŖŦ
ĄāĄĪADO=ĄĪ1ŖŦ
ĄßBD=DCŖŦ
ĄāĄĪ1=ĄĪCŖŦ
ĄāĄĪADO=ĄĪCŖŦ
Ķ֥ߥĪDOQ=ĄĪDPCŖŦ
ĄāĄ÷DOQĄ×Ą÷CPDŖŦ
Ąā![]() ŖŦ
ŖŦ
ĄßBD=DCŖŦ
Ąā![]() ŖŦ
ŖŦ
ĄāDQPC=BDDOŖģ
Ŗ¨3ŖŠ´æÔÚŖŦ
ĸŲČįÍŧ1ŖŦĩąĄĪBPO=90ĄãĘąŖŦ

ĄßBP=2tŖŦDQ=tŖŦ
ĄāAQ=8-t
Ąß´ËĘąAQ=BP
Ąā8-t=2t
ĄātŖŊ![]() Ŗģ
Ŗģ
ĸÚČįÍŧ2ŖŦĩąĄĪPOB=90ĄãĘąŖŦ

ĄßĄ÷DOQĄ×Ą÷BOP
Ąā![]()
ĄßAB=6ŖŦAD=8ŖŦ
ĄāBD=10ŖŦ
ĄāDO=![]()
ĄßĄ÷DOQĄ×Ą÷DBAŖŦ
Ąā![]() ŖŦ
ŖŦ
Ąā ŖŦ
ŖŦ
ĄātŖŊ![]() ŖŽ
ŖŽ
×ÛÉĪËųĘöŖŦĩątŖŊ![]() ÃëģōtŖŊ
ÃëģōtŖŊ![]() ÃëĘąŖŦĄ÷BOPÎĒÖąŊĮČũŊĮĐÎŖŽ
ÃëĘąŖŦĄ÷BOPÎĒÖąŊĮČũŊĮĐÎŖŽ

 ÔÄļÁŋėŗĩĪĩÁĐ´đ°¸
ÔÄļÁŋėŗĩĪĩÁĐ´đ°¸