Question

【题目】在矩形中，，，点在边上，且．

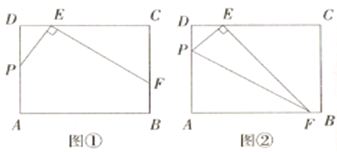
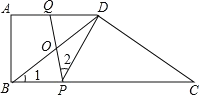
探究：如图①，点在矩形的边上，连结，过点作，交边于点．求证：．

应用：如图②，若图①的交边于点．其它条件不变，连结，则的值为 ，若的面积是．则的长为

Answer 1

【答案】探究：见解析；应用：，

【解析】

探究：根据同角的余角相等可得，结合可得；

应用：如图②，过点F作FG⊥CD于G，则，根据相似三角形的性质可得，设PE＝x，则EF＝3x，根据的面积是得出方程，求出PE，再利用勾股定理求出PD即可解决问题.

解：探究：∵四边形是矩形，

∴，

∴，

∵，

∴，

∴，

∴∽；

应用：如图②，过点F作FG⊥CD于G，则四边形GFBC是矩形，

∴FG＝BC＝AD＝3，

同探究可得：，

∴，

∵，

∴，

设PE＝x，则EF＝3x，

由题意得：，

解得：，

∴，

∴，

∴，

故答案为：，.