题目内容
如图，在Rt△AOB中，∠AOB=90°，OA=2，OB=1，∠XOA=30°，则A、B两点的坐标分别是________．
（
，1），（-
，
）
分析：作AC⊥x轴于点C，利用30°的正弦值和余弦值可点A的纵坐标和横坐标；作BD⊥x轴于点D，利用60°余弦值和正弦值可得OD，BD的长，根据象限内点的符号特点可得具体点的坐标．
解答：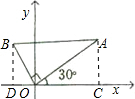
解：∵OA=2，∠XOA=30°，
∴AC=OA×sin30°=1，
OC=OA×cos30°=，
∴A（，1）；
∵∠BOD=60°，
OB=1，
∴OD=OB×cos60°=，
BD=OB×sin60°=，
∴B（-，），
故答案为（，1），（-，）．
点评：考查解直角三角形的知识；主要利用了30°，60°的特殊三角函数值求解．
，1），（-，）分析：作AC⊥x轴于点C，利用30°的正弦值和余弦值可点A的纵坐标和横坐标；作BD⊥x轴于点D，利用60°余弦值和正弦值可得OD，BD的长，根据象限内点的符号特点可得具体点的坐标．
解答：
解：∵OA=2，∠XOA=30°，∴AC=OA×sin30°=1，
OC=OA×cos30°=
，∴A（
，1）；∵∠BOD=60°，
OB=1，
∴OD=OB×cos60°=
，BD=OB×sin60°=
，∴B（-
，），故答案为（
，1），（-，）．点评：考查解直角三角形的知识；主要利用了30°，60°的特殊三角函数值求解．
练习册系列答案
相关题目
分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动，速度均为1cm/秒，设P、Q移动时间为t（0≤t≤4）
如图，在Rt△AOB中，∠ABO=90°，OB=4，AB=8，且反比例函数
（2013•咸宁）如图，在Rt△AOB中，OA=OB=3
（2013•南岗区一模）如图，在Rt△AOB中，∠AOB=90°，且AO=8，BO=6，P是线段AB上一个动点，PE⊥A0于E，PF⊥B0于F．设