题目内容
20.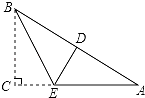 如图,在三角形纸片ABC中,∠C=90°,AC=12,折叠该纸片,使点C落在AB边上的D点处,折痕BE与AC交于点E,若AD=BD,则折痕BE的长为( )
如图,在三角形纸片ABC中,∠C=90°,AC=12,折叠该纸片,使点C落在AB边上的D点处,折痕BE与AC交于点E,若AD=BD,则折痕BE的长为( )| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
分析 如图,首先证明∠CBE=∠DBE(设为α),其次证明∠A=∠DBE=α;求出α=30°,得到CE=$\frac{1}{2}λ$;借助AC=12,求出λ即可解决问题.
解答  解:如图,由题意得:∠CBE=∠DBE(设为α),
解:如图,由题意得:∠CBE=∠DBE(设为α),
∠ADE=∠C=90°;
∵AD=BD,
∴BE=AE(设为λ),∠A=∠DBE=α;
∵∠C=90°,
∴2α+α=90°,
∴α=30°,CE=$\frac{1}{2}λ$;
∵AC=12,即λ+$\frac{1}{2}λ$=12,
∴λ=8.
故选B.
点评 该题主要考查了翻折变换的性质、直角三角形的边角关系等几何知识点及其应用问题;牢固掌握翻折变换的性质等几何知识点是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在平面直角坐标系中,点A(0,2),在x轴上任取一点M,连接AM,作AM的垂直平分线l1,过点M作x轴的垂线
l2.l1与l2交于点P.设P点的坐标为(x,y),那么x,y满足的关系式为( )
l2.l1与l2交于点P.设P点的坐标为(x,y),那么x,y满足的关系式为( )
| A. | y=$\frac{{x}^{2}}{4}$+1 | B. | y=x2+2x+1 | C. | y=2x2+1 | D. | y=x2+1 |
15. 由如图通过平移后可以得到的图案是( )
由如图通过平移后可以得到的图案是( )
 由如图通过平移后可以得到的图案是( )
由如图通过平移后可以得到的图案是( )| A. |  | B. |  | C. |  | D. |  |
10.一次函数y=kx-k的大致图象可能如图( )
| A. |  | B. |  | C. |  | D. |  |
 如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).