题目内容
7. 如图,AB∥CD,AE平分∠BAD交BC于E,BE=CE,求证:AD=AB+CD.
如图,AB∥CD,AE平分∠BAD交BC于E,BE=CE,求证:AD=AB+CD.
分析 延长DE与AB的延长线交于一点F,易证△DCE≌△FBE,可得BF=DC,则AF=AB+BF=AB+CD,又AB∥CD,AE平分∠BAD,可知∠ADF=∠AFD,则AD=AF.
解答 证明:延长DE与AB的延长线交于一点F,
∵AB∥CD,
∴∠CDE=∠BFE,
在△DCE和△FBE中,
$\left\{\begin{array}{l}{∠CDE=∠BFE}\\{∠DEC=∠FEB}\\{BE=CE}\end{array}\right.$,
∴△DCE≌△FBE,
∴BF=DC,
∴AF=AB+BF=AB+CD,
∵AE平分∠BAD,
∴∠ADF=∠AFD,
∴AD=AF,
∴AD=AB+CD.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△DCE≌△FBE是解题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
2.下列命题错误的是( )
| A. | 所有的实数都可用数轴上的点表示 | B. | 等角的补角相等 | ||
| C. | 无理数包括正无理数、0、负无理数 | D. | 对顶角相等 |
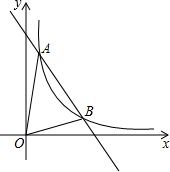 如图,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于A(1,6),B(3,n)两点.
如图,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于A(1,6),B(3,n)两点.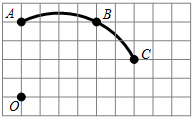 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点 A、B、C.其中点A的坐标为(0,4),
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点 A、B、C.其中点A的坐标为(0,4),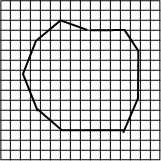 不规则面积的测量方法如下:把伞布放在方格纸上,在方格纸上描下它的轮廓,数一下图形中包含的方格数,对不满一格而大于半格的都算一格,小于半格的都舍去,总格数乘以每一格的面积,就是测量的总面积.在图中每小格的面积是1cm2,请估算不规则图形的面积约为100cm2.
不规则面积的测量方法如下:把伞布放在方格纸上,在方格纸上描下它的轮廓,数一下图形中包含的方格数,对不满一格而大于半格的都算一格,小于半格的都舍去,总格数乘以每一格的面积,就是测量的总面积.在图中每小格的面积是1cm2,请估算不规则图形的面积约为100cm2.