题目内容
如图，圆O是△ABC的外接圆，AB=AC，过点A作AP∥BC，交BO的延长线于点P．（1）求证：AP是圆O的切线；
（2）若圆O的半径R=5，BC=8，求线段AP的长．
【答案】分析：（1）由题意可知AE⊥BC且BE=CE，得出AE经过圆心O，只要证明AP⊥AE即可；
（2）可通过△APO∽△EBO及勾股定理求出AP的长．
解答：
（1）证明：过点A作AE⊥BC，交BC于点E，
∵AB=AC，
∴AE平分BC，
∴点O在AE上．（2分）
又∵AP∥BC，
∴AE⊥AP，
∴AP为圆O的切线．（4分）
（2）解：∵BE=
BC=4，
∴
，
又∵∠AOP=∠BOE，
∴△OBE∽△OPA，（6分）
∴
．
即
．
∴
．（8分）
点评：本题考查了切线的判定，先要证明AE经过圆心，再证明垂直即可．求AP的长，注意与已知线段相关的三角形联系，找准相似三角形．
（2）可通过△APO∽△EBO及勾股定理求出AP的长．
解答：
（1）证明：过点A作AE⊥BC，交BC于点E，∵AB=AC，
∴AE平分BC，
∴点O在AE上．（2分）
又∵AP∥BC，
∴AE⊥AP，
∴AP为圆O的切线．（4分）
（2）解：∵BE=
BC=4，∴
，又∵∠AOP=∠BOE，
∴△OBE∽△OPA，（6分）
∴
．即
．∴
．（8分）点评：本题考查了切线的判定，先要证明AE经过圆心，再证明垂直即可．求AP的长，注意与已知线段相关的三角形联系，找准相似三角形．
练习册系列答案
相关题目
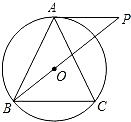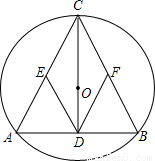
如图，圆O是△ABC的外接圆，AB=AC，过点A作AP∥BC，交BO的延长线于点P．
已知：如图，圆O是△ABC的外接圆，圆心O在这个三角形的高CD上，E、F分别是边AC和BC的中点，求证：四边形CEDF是菱形．
（2012•衡水一模）如图，圆O是△ABC的外接圆，连接OB、OC，圆O的半径R=10，sinA=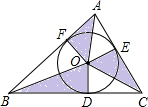
如图，圆O是△ABC的内切圆，与△ABC各边的切点分别为D、E、F，若图中3个阴影三角形的面积之和为4，内切圆半径为1，则△ABC的周长为（ ）