��Ŀ����
����Ŀ��У����ȫ�ǽ���������ע���ش����⣬��ȫ������Ҫ�dz��ٺͳ��أ�ij��ѧ��ѧ�С����������¼�·����ʻ�������ٶȵ�ʵ�飺���ڹ�·�Ա�ѡȡһ��C�����ڱ�ֱ�ij���l��ȷ����D��ʹCD��l��ֱ�����CD�ij�����24�ף���l�ϵ�D��ͬ��ȡ��A��B��ʹ��CAD��30������CBD��60����
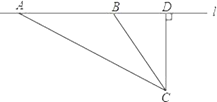
��1����AB�ij�������������ţ���
��2����֪��·�ζ�У������Ϊ45ǧ��/Сʱ�������ij��У����A��B��ʱ2�룬����У���Ƿ��٣�˵�����ɣ����ο����ݣ�![]() ��1.7��
��1.7��![]() ��1.4��
��1.4��
���𰸡���1��AB��16![]() �ף���2����У����AB·�γ��٣�
�ף���2����У����AB·�γ��٣�
��������
��1���ֱ���Rt��ADC��Rt��BDC��ͨ����������Ǻ������AD,BD�ij���Ȼ����AB��
��2����AB��������ʱ�����У�����ٶȣ�����45ǧ��/Сʱ���Ƚϼ���.
�⣺��1��������ã���Rt��ADC�У�tan30����![]() ��
��
���AD��![]() ��
��
��Rt��BDC ��tan60����![]() ��
��
���BD��![]() ,
,
����AB��AD��BD��![]() ���ף���
���ף���
��2��������A��B��ʱ2�룬�����ٶ�Ϊ![]() ��13.6����/�룩��
��13.6����/�룩��
��Ϊ13.6����/�룩��48.96ǧ��/Сʱ��45ǧ��/Сʱ
���Դ�У����AB·�γ��٣�

��ϰ��ϵ�д�
�����Ŀ