Question

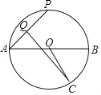
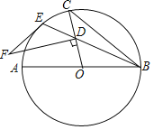
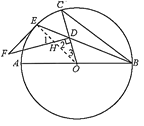
【题目】如图，AB是⊙O的直径，BE是弦，点D是弦BE上一点，连接OD并延长交⊙O于点C，连接BC，在过点D垂直于OC的直线上取点F．使∠DFE＝2∠CBE．

（1）请说明EF是⊙O的切线；

（2）若⊙O的半径是6，点D是OC的中点，∠CBE＝15°，求线段EF的长．

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）连接OE，由可得，由三角形内角和可得∠FEO=FDO=90°即可证明结论.

（2）由，可知∠DFE=∠3=30°，在中，可求出OH长，进而求出EH，再在Rt中求出EF即可.

（1）证明：如图，连接OE交DF于点H，

则．

∵，

∴．

∵，

∴．

∴．

又∵，

∴．

∴，即．

∵OE是的半径，

∴EF是的切线．

（2）解：∵，

∴．

∵的半径是6，点D是OC中点，

∴．

在中，，

∴．

∴．

在Rt中，，

．

∴．