Question

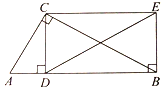
【题目】如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE，点F落在AD上．

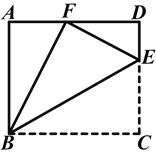
（1）求证：△ABF∽△DFE；

（2）若，求tan∠EBC的值．

Answer 1

【答案】见解析

【解析】

（1）证明：∵四边形ABCD是矩形，

∴∠A＝∠D＝∠C＝90°．

∵△BCE沿BE折叠为△BFE，∴∠BFE＝∠C＝90°．

∴∠AFB＋∠DFE＝180°－∠BFE＝90°．

又∠AFB＋∠ABF＝90°，

∴∠ABF＝∠DFE，∴△ABF∽△DFE．

（2）在Rt△DEF中，，

∴设DE＝a，则EF＝3a，

∴．

∵△BCE沿BE折叠为△BFE，

∴CE＝EF＝3a，∠EBC＝∠EBF，

∴CD＝DE＋CE＝4a，

∴AB＝4a．

又由（1）知△ABF∽△DFE，

∴．

∴，即．