题目内容
在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为 上﹣
上﹣
点,且 =
= 连接DF,并延长DF交BA的延长线于点E.
连接DF,并延长DF交BA的延长线于点E.
(1)判断DB与DA的数量关系,并说明理由;
(2)求证:△BCD≌△AFD;
(3)若∠ACM=120°,⊙O的半径为5,DC=6,求DE的长.

解:(1)DB=DA.
理由:∵CD是△ABC的外角平分线,
∴∠MCD=∠ACD,
∵∠MCD+∠BCD=180°,∠BCD+∠BAD=180°,
∴∠MCD=∠BAD,
∴∠ACD=∠BAD,
∵∠ACD=∠ABD,
∴∠ABD=∠BAD,
∴ DB=DA;
DB=DA;
(2)证明:∵DB=DA,
∴ =
= ,
,
∵ =
= ,
,
∴AF=BC, =
= ,
,
∴CD=FD,
在△BCD和△AFD中,
 ,
,
∴△BCD≌△AFD(SSS);
(3)连接DO并延长,交AB于点N,连接OB,
∵DB=DA,
∴ =
= ,
,
∴DN⊥AB,
∵∠ACM=120°,
∴∠ABD=∠ACD=60° ,
,
∵DB=DA,
∴△ABD是等边三角形,
∴∠OBA=30°,
∴ON= OB=
OB= ×5=2.5,
×5=2.5,
∴DN=ON+OD=7.5,
∴BD= =5
=5 ,
,
∴AD=BD=5 ,
,
∵ =
= ,
,
∴ =
= ,
,
∴∠ADC=∠BDF,
∵∠ABD=∠ACD,
∴△ACD∽△EBD,
∴ ,
,
∴ ,
,
∴DE=12.5.


练习册系列答案
相关题目



 cm,则正六边形的半径为
cm,则正六边形的半径为 

 B. 3 C.
B. 3 C.  D. 2
D. 2
 =
= ,则ad=bc;
,则ad=bc; 中,自变量
中,自变量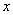 的取值范围是__________.
的取值范围是__________.