题目内容
用甲、乙两种原料配制成一种饮料，已知两种原料中的维生素C和维生素E及购买这两种原料的价格如下表：
| 甲种原料 | 乙种原料 | |
| 维生素C含量（单位/千克） | 600 | 100 |
| 维生素E含量（单位/千克） | 300 | 500 |
| 原料价格（元/千克） | 15 | 5 |
（2）按照（1）中最低成本配制的饮料售价定为每瓶8元（0.5千克每瓶），每天可售出80瓶，若售价每上涨0.5元，则每天可少售出10瓶，问定价多少元时，每天的利润最大？最大利润是多少？
解：（1）设需要甲种原料x千克，则乙原料（10-x）千克，
由题意得，
，
解得：6.4≤x≤23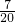
，
成本=15x+5（10-x）=10x+50，
∵10＞0，成本随x的增大而增大，
∴当x=7时，成本最低，最低成本=15×7+5×3=120元．
（2）由（1）得，每千克的成本为12元，则一瓶的成本为6元，
设定价为x，利润为w，
则w=（x-6）×（80-
×10）=-20（x-9）2+180，
当x=9时，利润最大，最大利润为180元．
答：定价9元时，每天的利润最大，最大利润是180元．
分析：（1）设需要甲种原料x千克，则乙原料（10-x）千克，根据至少含有4200单位维生素C和330单位维生素E，可得出x的取值，再由要求成本最低，可确定x的取值，也可得出每千克的最低成本；
（2）根据（1）求出一瓶的成本，设定价为x，利润为w，从而得出w关于x的二次函数，利用配方法求最值即可．
点评：本题考查了二次函数的应用、一元一次不等式组的应用，解答本题的关键是仔细审题，建立数学模型，将实际问题转变为数学问题求解．
由题意得，
，解得：6.4≤x≤23
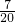，成本=15x+5（10-x）=10x+50，
∵10＞0，成本随x的增大而增大，
∴当x=7时，成本最低，最低成本=15×7+5×3=120元．
（2）由（1）得，每千克的成本为12元，则一瓶的成本为6元，
设定价为x，利润为w，
则w=（x-6）×（80-
×10）=-20（x-9）2+180，当x=9时，利润最大，最大利润为180元．
答：定价9元时，每天的利润最大，最大利润是180元．
分析：（1）设需要甲种原料x千克，则乙原料（10-x）千克，根据至少含有4200单位维生素C和330单位维生素E，可得出x的取值，再由要求成本最低，可确定x的取值，也可得出每千克的最低成本；
（2）根据（1）求出一瓶的成本，设定价为x，利润为w，从而得出w关于x的二次函数，利用配方法求最值即可．
点评：本题考查了二次函数的应用、一元一次不等式组的应用，解答本题的关键是仔细审题，建立数学模型，将实际问题转变为数学问题求解．
练习册系列答案
阅读快车系列答案
相关题目
某厂用甲、乙两种原料配制成某种饮料，已知这两种原料中的维生素C含量及每千克原料的价格如下表所示：
现配制这种饮料10kg，要求至少含有4200单位的维生素C，并要求购买甲、乙两种原料的费用不超过72元，请根据以上条件解答下列问题：
（1）设需用xkg甲种原料，写出x所满足的不等式组；
（2）若按上述条件购买甲种原料的质量为整kg数，有几种购买方案，请写出购买方案．
| 原料项目 | 甲种原料 | 乙种原料 |
| 维生素C含量 （单位/kg） | 600 | 100 |
| 原料价格（元/kg） | 8 | 4 |
（1）设需用xkg甲种原料，写出x所满足的不等式组；
（2）若按上述条件购买甲种原料的质量为整kg数，有几种购买方案，请写出购买方案．
用甲、乙两种原料配制成某种饮料，已知这两种原料的维生素C含量及购买这两种原料的价格如下现配制这种饮料10千克，要求至少含有4000单位的维生素C，并且购买甲、乙两种原料的费用不超过72元，若购买甲种原料的质量为x（整数）千克，请解答下列问题：
（1）购买甲、乙两种原料有哪几种方案？
（2）哪种购买方案的费用最低？最低费用是多少元？
| 甲种原料 | 乙种原料 | |
| 维生素C/（单位/千克） | 600 | 100 |
| 原料价格/（元/千克） | 8 | 4 |
（2）哪种购买方案的费用最低？最低费用是多少元？