题目内容
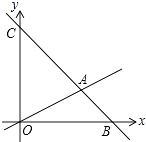
【题目】要在街道旁修建一个奶站，向居民区A，B提供牛奶，奶站应建在什么地方，才能使从A，B到它的距离之和最短？小聪根据实际情况，以街道旁为x轴，建立了如图所示的平面直角坐标系，测得A点的坐标为(0，3)，B点的坐标为(6，5)，则从A，B两点到奶站距离之和的最小值是( )
A. 7 B. 9 C. 8 D. 10
【答案】D
【解析】
可先找点A关于x轴的对称点A′，因为两点之间线段最短，连接A′B，即为最短距离．
如图,取A关于x轴的对称点A′，
连接A′B交x轴于点C，
∵A点的坐标为(0,3)，
∴A′点的坐标为(0,3)，
则点C为从A. B两点到奶站距离之和的最小的点，
在Rt△A′BD中，
A′B＝
＝10，
所以最短距离为10.
故选D.
练习册系列答案
相关题目
