题目内容
 如图,直角梯形ABCD中,AD∥BC,∠B=90°,∠DCB=45°,AD=3.5cm,DC=5
如图,直角梯形ABCD中,AD∥BC,∠B=90°,∠DCB=45°,AD=3.5cm,DC=5| 2 |
考点:轴对称-最短路线问题,直角梯形
专题:
分析:利用轴对称求最短路线的做法得出P点位置,进而利用勾股定理得出CD′的长,即为PD+PC的最小值.
解答: 解:过点D作DF⊥BC于点F,作D点与AB的对称点D′,过点D′向BC作垂线于点E,
解:过点D作DF⊥BC于点F,作D点与AB的对称点D′,过点D′向BC作垂线于点E,
∵∠DCB=45°,DC=5
cm,
∴DF=FC=
×5
=5(cm),
∵AD=3.5cm,
∴AD′=BF=BE=3.5cm,
∴CD′=
=
=13(cm),
∴PD+PC的最小值为:13.
 解:过点D作DF⊥BC于点F,作D点与AB的对称点D′,过点D′向BC作垂线于点E,
解:过点D作DF⊥BC于点F,作D点与AB的对称点D′,过点D′向BC作垂线于点E,∵∠DCB=45°,DC=5
| 2 |
∴DF=FC=
| ||
| 2 |
| 2 |
∵AD=3.5cm,
∴AD′=BF=BE=3.5cm,
∴CD′=
| D′E2+EC2 |
| 52+122 |
∴PD+PC的最小值为:13.
点评:此题主要考查了利用轴对称求最短路径问题,利用已知得出P点位置是解题关键.

练习册系列答案
相关题目
已知关于x的方程x2-(k+2)x+2k+1=0的两实数根为x1,x2,若x12+x22=11,则实数k的值为( )
| A、-3 | B、3 | C、±3 | D、无解 |
下列说法正确的是( )
| A、对应边成比例的多边形都相似 |
| B、四个角对应相等的梯形都相似 |
| C、有一个角相等的两个菱形相似 |
| D、有一个锐角相等的两个等腰三角形相似 |
 二次函数y=x2+bx+c的图象经过点A(4,3),B(1,0).
二次函数y=x2+bx+c的图象经过点A(4,3),B(1,0). 如图,在某高速公路上从3千米处开始,每隔4千米设置一个速度限制标志,而且从10千米处开始,每隔9千米设置一个测速照相机标志,则刚好在19千米处同时设置这两种标志.那么下一个同时设置这两种标志的地点的千米数是
如图,在某高速公路上从3千米处开始,每隔4千米设置一个速度限制标志,而且从10千米处开始,每隔9千米设置一个测速照相机标志,则刚好在19千米处同时设置这两种标志.那么下一个同时设置这两种标志的地点的千米数是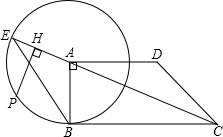 如图,已知直角梯形ABCD中,AD∥BC,∠DAB=90°,且AD=DC,以A为圆心,AB为半径作⊙A,交CA延长线于点E.
如图,已知直角梯形ABCD中,AD∥BC,∠DAB=90°,且AD=DC,以A为圆心,AB为半径作⊙A,交CA延长线于点E.
 如图,甲转盘被分成3个面积相等的扇形,乙转盘被分成2个半圆,每一个扇形或半圆都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转一次,直到指针指向一个区域为止).
如图,甲转盘被分成3个面积相等的扇形,乙转盘被分成2个半圆,每一个扇形或半圆都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转一次,直到指针指向一个区域为止). 如图,P是正方形ABCD的对角线BD上一点,过点P作EF、MN分别平行BC、AB,交两组对边于E、F、M、N,则四边形EBMP和PFDN都是正方形,设正方形EBMP的边长为a,正方形PFDN的边长为b.
如图,P是正方形ABCD的对角线BD上一点,过点P作EF、MN分别平行BC、AB,交两组对边于E、F、M、N,则四边形EBMP和PFDN都是正方形,设正方形EBMP的边长为a,正方形PFDN的边长为b.