题目内容

1．观察下列等式，你会发现什么规律：1×3+1=22，2×4+1=32，3×5+1=42…请将你发现的规律用只含一个字母n（n为正整数）的等式表示出来n（n+2）+1=（n+1）2．

分析 因为由题目中的数据可知1×（1+2）+1=（1+1）2；2×（2+2）+1=（1+2）2；3×（3+2）+1=（1+3）2；所以可据此推出第n个式子为n（n+2）+1=（n+1）2．

解答 解：∵1×（1+2）+1=（1+1）2，2×（2+2）+1=（1+2）2，3×（3+2）+1=（1+3）2，
∴第n个式子为n（n+2）+1=（n+1）2，
故答案为：n（n+2）+1=（n+1）2．

点评 本题主要考查了数字的变化规律，观察、分析已知数据，寻找它们之间的相互联系，探寻其规律：第n个式子为n（n+2）+1=（n+1）2是解答此题的关键．

练习册系列答案
相关题目
14．如图，AB∥CD，∠BAE=∠DCE=45°，则∠E=90°．
12．二次函数y=-$\frac{1}{2}{x^2}$-3x+8的图象与x轴交于A、B两点（点A在B的左侧），与y轴交于点C，此抛物线的顶点为点D，对称轴交x轴于点E，如图①．
（1）求AC的解析式和抛物线的顶点D的坐标．
（2）点F是抛物线上直线AC上方的一点，求：当△ACF的面积最大时，点F的坐标，并求出△ACF的最大面积．
（3）如图②，点H的坐标是（0，6）连接EH和BH，将△EBH沿直线EH翻折，点B的对应点为点G，作直线CG，在直线CG上是否存在一点M，使得△EHM是直角三角形？若存在，直接写出点M的坐标，若不存在，请说明理由．
9．等腰三角形的底角为80°，则它的顶角是（　　）
A．80°B．60°C．40°D．20°
16．下两中学初一年级在国庆前举行了秋季拔河比赛．甲、乙两班进入最后决赛．随着裁判的一声哨响，标志物先向乙队移动了0.2米．又向甲队方向移动了0.5米，又向乙队方向移动了0.4米，随后又向甲队方向移动了1.3米，在大家的欢呼中又向甲队方向移动了0.9米．若规定标志物向某队移动2米该队就获胜，那么哪队最后取得了胜利？
6．若多项式x2+kx+25是一个多项式的平方，则k=±10．
13．直线y=$\frac{1}{2}$x+2与x轴，y轴分别相交于A、B两点，与反比例函数y=$\frac{k}{x}$（x＞0）的图象相交于点C（2，3）．点P是反比例函数图象上一点，作PE垂直x轴于E，若以P、O、E为顶点的三角形与△AOB相似，则点P的坐标是（2$\sqrt{3}$，$\sqrt{3}$），（$\sqrt{3}$，2$\sqrt{3}$）．
10．反比例函数$y=-\frac{2}{x}$图象上有三点$A（-\frac{1}{2}，{y_1}）$、B（-1，y2）、$B（\frac{1}{3}，{y_3}）$，则y1、y2、y3的大小关系是（　　）
A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y1＜y2D．y3＜y2＜y1
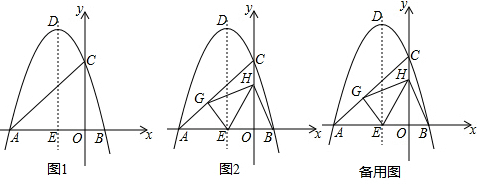
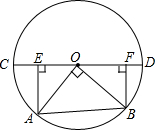8．如图，CD为⊙O的直径，OA，OB是⊙O的半径，OA⊥OB，作AE⊥CD于E，BF⊥CD于F，已知AB=5$\sqrt{2}$．求CE+AE+BF+DF的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网