题目内容
已知：如图，⊙A与y轴交于C、D两点，圆心A的坐标为（1，0），⊙A的半径为| 5 |
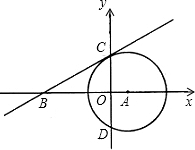过C作⊙A的切线交x轴于点B．（1）求切线BC的解析式；
（2）若点P是第一象限内⊙A上的一点，过点P作⊙A的切线与直线BC相交于点G，且∠CGP=120°，求点G的坐标；
（3）向左移动⊙A（圆心A始终保持在x轴上），与直线BC交于E、F，在移动过程中是否存在点A，使△AEF是直角三角形？若存在，求出点A的坐标；若不存在，请说明理由．
分析：（1）连接AC，由勾股定理可求出OC的长，进而得出C点坐标，同理，由切线的性质及勾股定理即可得出OB的长，进而求出B点坐标，再用待定系数法即可求出过BC两点的直线解析式；
（2）过G点作x轴垂线，垂足为H，连接AG，设G（x0，y0），在Rt△ACG中利用锐角三角函数的定义可求出CG的长，
由勾股定理可得出BC的长，由OC∥GH可得出
=
，进而可求出G点坐标；
（3）假设△AEF为直角三角形，由AE=AF可判断出△AEF为等腰三角形，可得出∠EAF=90°，过A作AM⊥BC于M，
在Rt△AEF中利用勾股定理可求出EF的长度，证出△BOC∽△BMA，由相似三角形的性质可得出A点坐标；当圆心A在点B的左侧时，设圆心为A′，过A′作A′M′⊥BC于M′，可得△A′M′B′≌△AMB，由全等三角形的性质可得出A′点的坐标．
（2）过G点作x轴垂线，垂足为H，连接AG，设G（x0，y0），在Rt△ACG中利用锐角三角函数的定义可求出CG的长，
由勾股定理可得出BC的长，由OC∥GH可得出
| OH |
| BO |
| CG |
| BC |
（3）假设△AEF为直角三角形，由AE=AF可判断出△AEF为等腰三角形，可得出∠EAF=90°，过A作AM⊥BC于M，
在Rt△AEF中利用勾股定理可求出EF的长度，证出△BOC∽△BMA，由相似三角形的性质可得出A点坐标；当圆心A在点B的左侧时，设圆心为A′，过A′作A′M′⊥BC于M′，可得△A′M′B′≌△AMB，由全等三角形的性质可得出A′点的坐标．
解答：解：（1）连接AC，则OC=
=2，故点C的坐标为（0，2），
∵BC为⊙O的切线，
∴AC⊥BC，
在Rt△ABC中，（OB+OA）2=BC2+AC2，即（OB+1）2=BC2+5①，
在Rt△OBC中，BC2=OB2+OC2，即OBC2=OB2+4②，
①②联立得，OB=4，
∴点B的坐标为（-4，0）
∴直线BC的解析式为y=
x+2；
（2）如图1：
解法一：过G点作x轴垂线，垂足为H，连接AG，设G（x0，y0），
在Rt△ACG中，∠AGC=60°，AC=
，求得CG=
，
又∵OB=4，
∴BC=
=2
，
∵OC∥GH，
∴
=
，则OH=
，即x0=
，
又∵点G在直线BC上，
∴y0=
×
+2
=
+2，
∴G（
，
+2），
解法二：过G点作y轴垂线，垂足为H，连接AG
在Rt△ACG中，∠AGC=60°，AC=
，求得CG=
，
由△BCO∽△GCH，得
=
=
，
即GH=2CH，
在Rt△CHG中，CG=
，GH=2CH，得CH=
，HG=
，
∴G（
，
+2）；
（3）方法一
如图2：
在移动过程中，存在点A，使△AEF为直角三角形．
若△AEF为直角三角形
∵AE=AF
∴△AEF为等腰三角形，
∴∠AEF=∠AFE≠90°，
∴∠EAF=90°，
过A作AM⊥BC于M，
在Rt△AEF中，EF=
=
=
，
AM=
EF=
，
证出△BOC∽△BMA得，
=
，
而BC=
=
=2
，OC=2，可得AB=
∴OA=4-
，
∴A（-4+
，0），
当圆心A在点B的左侧时，设圆心为A′，
过A′作A′M′⊥BC于M′，可得△A′M′B′≌△AMB，
∴A′B=AB=
，
∴OA′=OB+A′B=4+
，
∴A′（-4-
，0），
∴A（-4+
，0）或A′（-4-
，0）
方法二：
如图3，
在移动过程中，存在点A，使△AEF为直角三角形
若△AEF为直角三角形
∵AE=AF
∴△AEF为等腰三角形
∴∠AEF=∠AFE≠90°
∴∠EAF=90°（11分）
过F作FM⊥x轴于M，EN⊥x轴于N，EH⊥MF于H
设AN=x，EN=y
由△AEN≌△FAM
可得AM=y，FM=x
FH=x-y
EH=x+y，由
=
=
=
，即
=
，
∴x=3y
在Rt△AEN中，
x2+y2=（
）2
x2+y2=5，
解得
，
又∵
=
=
=
，
∴BN=2y，BN=
，
∴AB=
+
=
，
∴OA=4-
，
∴A（-4+
，0），
以下同解法一，得A′（-4-
，0）．（16分）
(
|
∵BC为⊙O的切线，
∴AC⊥BC，
在Rt△ABC中，（OB+OA）2=BC2+AC2，即（OB+1）2=BC2+5①，
在Rt△OBC中，BC2=OB2+OC2，即OBC2=OB2+4②，
①②联立得，OB=4，
∴点B的坐标为（-4，0）
∴直线BC的解析式为y=
| 1 |
| 2 |
（2）如图1：
解法一：过G点作x轴垂线，垂足为H，连接AG，设G（x0，y0），在Rt△ACG中，∠AGC=60°，AC=
| 5 |
| ||
| 3 |
又∵OB=4，
∴BC=
| OB2+OC2 |
| 5 |
∵OC∥GH，
∴
| OH |
| BO |
| CG |
| BC |
2
| ||
| 3 |
2
| ||
| 3 |
又∵点G在直线BC上，
∴y0=
| 1 |
| 2 |
2
| ||
| 3 |
=
| ||
| 3 |
∴G（
2
| ||
| 3 |
| ||
| 3 |
解法二：过G点作y轴垂线，垂足为H，连接AG
在Rt△ACG中，∠AGC=60°，AC=
| 5 |
| ||
| 3 |
由△BCO∽△GCH，得
| CH |
| GH |
| CO |
| BO |
| 1 |
| 2 |
即GH=2CH，
在Rt△CHG中，CG=
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
∴G（
2
| ||
| 3 |
| ||
| 3 |
（3）方法一
如图2：
在移动过程中，存在点A，使△AEF为直角三角形．若△AEF为直角三角形
∵AE=AF
∴△AEF为等腰三角形，
∴∠AEF=∠AFE≠90°，
∴∠EAF=90°，
过A作AM⊥BC于M，
在Rt△AEF中，EF=
| AE2+AF2 |
(
|
| 10 |
AM=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
证出△BOC∽△BMA得，
| OC |
| AM |
| BC |
| AB |
而BC=
| OC2+OB2 |
| 22+42 |
| 5 |
5
| ||
| 2 |
∴OA=4-
5
| ||
| 2 |
∴A（-4+
5
| ||
| 2 |
当圆心A在点B的左侧时，设圆心为A′，
过A′作A′M′⊥BC于M′，可得△A′M′B′≌△AMB，
∴A′B=AB=
5
| ||
| 2 |
∴OA′=OB+A′B=4+
5
| ||
| 2 |
∴A′（-4-
5
| ||
| 2 |
∴A（-4+
5
| ||
| 2 |
5
| ||
| 2 |
方法二：
如图3，
在移动过程中，存在点A，使△AEF为直角三角形
若△AEF为直角三角形
∵AE=AF
∴△AEF为等腰三角形
∴∠AEF=∠AFE≠90°
∴∠EAF=90°（11分）
过F作FM⊥x轴于M，EN⊥x轴于N，EH⊥MF于H
设AN=x，EN=y
由△AEN≌△FAM
可得AM=y，FM=x
FH=x-y
EH=x+y，由
| FH |
| EH |
| OC |
| OB |
| 2 |
| 4 |
| 1 |
| 2 |
| x-y |
| x+y |
| 1 |
| 2 |
∴x=3y
在Rt△AEN中，
x2+y2=（
| 5 |
x2+y2=5，
解得
|
又∵
| EN |
| BN |
| OC |
| OB |
| 2 |
| 4 |
| 1 |
| 2 |
∴BN=2y，BN=
| 2 |
∴AB=
3
| ||
| 2 |
| 2 |
5
| ||
| 2 |
∴OA=4-
5
| ||
| 2 |
∴A（-4+
5
| ||
| 2 |
以下同解法一，得A′（-4-
5
| ||
| 2 |
点评：本题考查的是切线的性质及相似三角形的判定与性质、全等三角形的判定与性质，待定系数法求一次函数的解析式，涉及面较广，难度较大．
练习册系列答案
名校课堂系列答案
相关题目
21、已知：如图，⊙O1与⊙O2相交于A、B两点，过A的直线交⊙O1于C，交⊙O2于D，过B的直线交⊙O1于E，交⊙O2于F，且CD∥EF．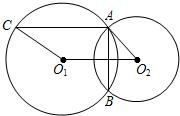
，⊙O2的半径为
14、已知：如图，⊙O1与⊙O2外切于点P，⊙O1的半径为3，且O1O2=8，则⊙O2的半径R=
（1997•南京）已知：如图，⊙O1与⊙O2外切于点P，A为⊙O1上一点，直线AC切⊙O2于点C，且交⊙O1于点B，AP的延长线交⊙O2于点D．
已知：如图，⊙O1与⊙O2相交于A，B两点．求证：直线O1O2垂直平分AB．